Игра "Жизнь" на языке Wolfram Mathematica
- Правила игры “Жизнь”
- Игра “Жизнь” на языке MATLAB
- Игра “Жизнь” на языке Python
- Игра “Жизнь” на языке SQL
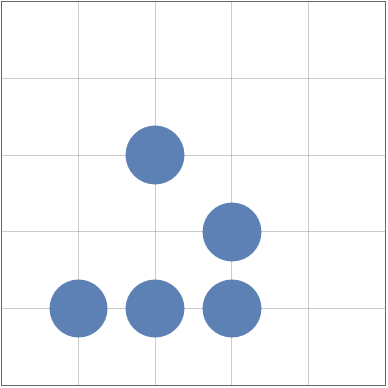
Колонию будет задавать списком пар координат “живых” клеток. Например, колония “Глайдер” может быть представлена списком:
colony = {{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 2}};
Построим изображение этой колонии при помощи функции ListPlot:
ListPlot[colony, PlotStyle -> PointSize[0.15],
PlotRange -> {{-1, 4}, {-1, 4}}, AspectRatio -> 1, Frame -> True,
Axes -> False, GridLines -> {Range[-1, 4]}]
Функция определения принадлежности клетки колонии: используем функцию MemberQ
Для проверки принадлежности клетки x колонии col будем использовать функцию MemberQ, которая возвращает True если элемент, указанный вторым аргументом, будет принадлежать списку, указанному первым аргументом и False если элемент не найден в списке. Для рассматриваемой колонии:
MemberQ[colony,{1, 0}]
>> True
MemberQ[colony,{5, 0}]
>> False
Считаем количество соседей: Используем функции Tuples, Count и Map
Для определения количества соседей у некоторой клетки или пустой ячейки с координатами c = (x, y) необходимо определить список координат смежных ячеек (ячеек-соседей) и подсчитать в этом списке количество ячеек, занятых клетками.
Вокруг каждой клетки 8 смежных ячеек, с которыми она граничит. Координатны смежных ячеек отличаются от координаты клетки не более чем на 1. Например, список координат соседних ячеек для клетки с координатами (2,3):
{{1, 2}, {1, 3}, {1, 4}, {2, 2}, {2, 4}, {3, 2}, {3, 3}, {3, 4}}
Для получения списка пар координат смежных ячеек используем функцию Tuples, которая позволяет создать список всех возможных кортежей, состоящих из двух 2 элементов, составленных из элементов заданного списка. Первым аргументом в функцию Tuples передаём список смещений координат смежных ячеек относительно рассматриваемой клетки (-1, 0, 1), вторым аргументом число 2, определяющее длину кортежей. На выходе получаем все возможные пары смещений координат:
Tuples[{-1, 0, 1}, 2]
>> {{-1,-1}, {-1,0}, {-1,1}, {0,-1}, {0,0}, {0,1}, {1,-1}, {1,0}, {1,1}}
Для исключения из этого списка пары с нулевым смещением (0,0) используем функцию DeleteCases, которая позволяет удалить из списка элемент.
DeleteCases[ Tuples[{-1, 0, 1}, 2], {0,0} ]
>> {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}}
Если каждую полученную пару смещений прибавить к координатам (x,y), получим список координат клеток, смежных клетке (x,y)
{x, y} + # & /@ Tuples[{-1, 0, 1}, 2]
>> {{-1+x,-1+y}, {-1+x,y}, {-1+x,1+y}, {x,-1+y}, {x,y}, {x,1+y}, {1+x,-1+y}, {1+x,y}, {1+x,1+y}}
Каждую клетку этого списка проверим на принадлежность колонии и подсчитаем количество результатов True. Для подсчета элементов в списке, удовлетворяющим заданному условию, используем функцию Count:
Count[{True, False, False, False, False, False, False, False}, True]
>> 1
Создадим функцию подсчёта количества соседей, окружающих ячейку с координатами c = {x, y}:
countNeighbours[c_, colony_] := Count[MemberQ[colony, c + #] & /@ Tuples[{-1, 0, 1}, 2], True];
countNeighbours[{1, 1}, colony]
>> 5
Ареал колонии
Ареал колонии это множество клеток колонии и всех их смежных ячеек. Для каждой ячейки, принадлежащей ареалу колонии, определяется количество соседей и, в зависимости от этого количества и того пустая эта ячейка или занята клеткой принимается решение о появлении новой клетки или переходе существующей в следующее поколение.
Для определения арела колонии сформируем списки смежных ячеек для всех клеток колонии, включив в эти списки и клетки колонии. Для формирования таких списков используем функцию Outer[f,list1,list2,list3,…], которая формирует все возможные комбинации элементов списков самого низкого уровня в каждом из списков и передаёт эти комбинации в качестве аргументов в функцию f.
Outer[f, {{1, 2}, {3, 4}}, {{10, 20}}]
>> {{{{f[1, 10], f[1, 20]}}, {{f[2, 10], f[2, 20]}}}, {{{f[3, 10], f[3, 20]}}, {{f[4, 10], f[4, 20]}}}}
Чтобы Математика рассматривала списки на уровне 1 как элементы, списков, необходимо указать номер этого уровня последним аргументом:
Outer[f, {{1, 2}, {3, 4}}, {{10, 20}}, 1]
>> {{f[{1, 2}, {10, 20}]}, {f[{3, 4}, {10, 20}]}}
В качестве функции f используем “чистую” функцию сложения элементов двух списков. Второй аргумент функции Outer список координат клеток колонии, третий – список смещений.
Outer[#1 + #2 &, colony, Tuples[{-1, 0, 1}, 2], 1]
Получившийся список многомерный. Сделаем его “плоским” при помощи функции Flatten:
Flatten[Outer[f, {{1, 2}, {3, 4}}, {{10, 20}}, 1]]
>> {f[{1, 2}, {10, 20}], f[{3, 4}, {10, 20}]}
Записанное выше выражение вернет список всех смежных клеток для всех клеток колонии, в котором будут повторения. Эти повторения можно исключить, используя функцию для работы с множествами Union, которая при вызове с одним аргументом удаляет повторы элементов.
colonyArea[colony_] := Union[Flatten[Outer[#1 + #2 &, colony, Tuples[{-1, 0, 1}, 2], 1], 1]];
Функция nextGeneration. Используем функции Union, Select и Map
На основе списка координат ячеек ареала колонии создадим список, каждый элемент которого будет представлять собой кортеж из трех элементов: координаты ячейки, количество соседей, признак занятости ячейки клеткой.
{#, countNeighbours[#, colony], MemberQ[colony, #]} & /@ colonyArea[colony]
>> {{{-1, -1}, 1, False}, {{-1, 0}, 1, False}, {{-1, 1}, 1,
False}, {{0, -1}, 2, False}, {{0, 0}, 2, True}, {{0, 1}, 3,
False}, {{0, 2}, 1, False}, {{0, 3}, 1, False}, {{1, -1}, 3,
False}, {{1, 0}, 4, True}, {{1, 1}, 5, False}, {{1, 2}, 2,
True}, {{1, 3}, 1, False}, {{2, -1}, 2, False}, {{2, 0}, 3,
True}, {{2, 1}, 4, True}, {{2, 2}, 2, False}, {{2, 3}, 1,
False}, {{3, -1}, 1, False}, {{3, 0}, 2, False}, {{3, 1}, 2,
False}, {{3, 2}, 1, False}}
Из получившегося списка при помощи функции Select выберем только те ячейки, у который ровно три соседа (это или новые клетки или “выжившие” клетки, у которых три соседа) и клетки (занятые ячейки) у которых ровно два соседа.
Select[..., #[[2]] == 3 || (#[[2]] == 2 && #[[3]]) &]
Вместо многоточия подставим полученное еще выше выражение для генерации списка 3-кортежей. Результатом работы функции Select также будет список 3-кортежей, из которого нам необходимо извлечь только первый элемент:
nextGeneration[colony_] := #[[1]] & /@
Select[{#, countNeighbours[#, colony], MemberQ[colony, #]} & /@
colonyArea[colony], #[[2]] == 3 || (#[[2]] == 2 && #[[3]]) &]
Функция NestList. Формирование списка поколений
Функция NestList[f,x,n] формирует список результатов применения функции f к выражению x от 0 до n раз
NestList[f, x, 4];
>> {x, f[x], f[f[x]], f[f[f[x]]], f[f[f[f[x]]]]}
Используем эту функцию для создания списка поколений колонии
generationList = NestList[nextGeneration, colony, 100];
Результат
Создадим более сложную колонию:
colony = {{0, 0}, {1, 0}, {2, 0}, {2, 1}, {1, 2}, {4, -1}, {4, -2}, {4, -3}};
ListPlot[colony, PlotStyle -> PointSize[0.1],
PlotRange -> {{-2, 6}, {-4, 5}}, AspectRatio -> 1,
Frame -> True, Axes -> False, GridLines -> {Range[-3, 4]},
FrameTicks -> None]
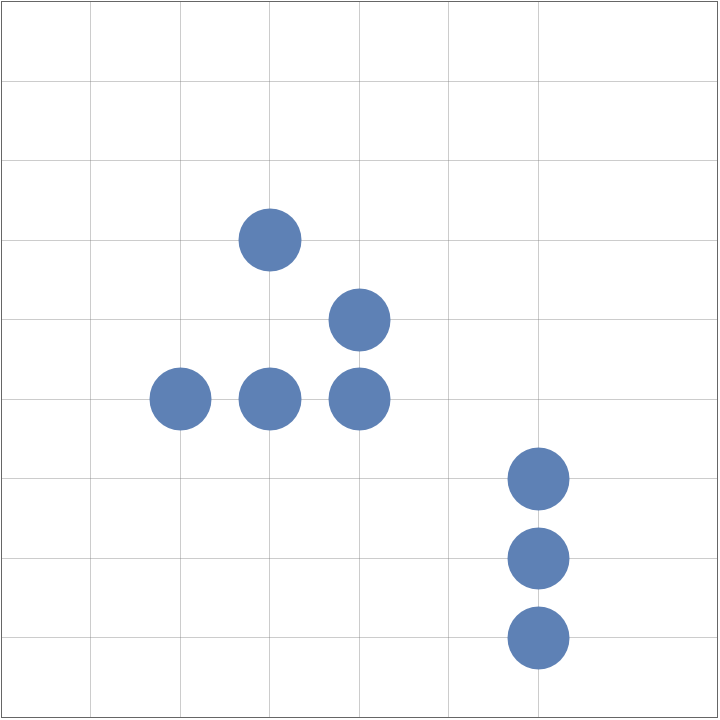
Сгенерируем список поколений и построим анимацию “эволюции” этой колонии:
NestList[nextGeneration, colony, 600];
Animate[ListPlot[%[[i]], PlotStyle -> PointSize[0.01],
PlotRange -> {{-50, 50}, {-50, 50}}, AspectRatio -> 1,
Axes -> False, Frame -> True, FrameTicks -> None], {i, 1, 600, 1},
DisplayAllSteps -> True]

