Построение модели сети для захвата объекта космического мусора
Построение модели сети для захвата объекта космического мусора. Сеть рассматривается как система материальных точек, связанных невесомыми пружинами. Записывается система уравнений движения сети при её взаимодействии с объектом. Приведен пример программы на языке MATLAB/Octave, которая иллюстрирует работу модели.
Известны различные способы захвата и увода с орбиты крупных объектов космического мусора. Для захвата могут использоваться манипуляторы, гарпуны, специальные стыковочные устройства, для орбитальной транспортировки – тросовые системы, сила Кулона, потоки частиц.

Один из перспективных способов безопасного захвата крупногабаритных объектов предполагает использование сети. Сеть, связанная тросом с космическим буксиром, выбрасывается в направлении объекта космического мусора, раскрывается в процессе сближения с ним и выполняет захват. После захвата космический буксир транспортирует захваченный объект космического мусора на орбиту утилизации или захоронения.

Сетью можно захватывать вращающиеся объекты, захват которых при помощи манипуляторов или других жестких механизмов может привести к значительным ударным нагрузкам при контакте устройства захвата с объектом.
Модель сети
Для анализа движения сети и её взаимодействия с объектом космического мусора часто используется упрощенная модель, которая представляет сеть в виде системы материальных точек, связанных упругими безмассовыми элементами – пружинами (mass spring model). Материальные точки располагаются в узлах сети, а также между узлами для более точного моделирования взаимодействия сети с поверхностью объекта космического мусора.
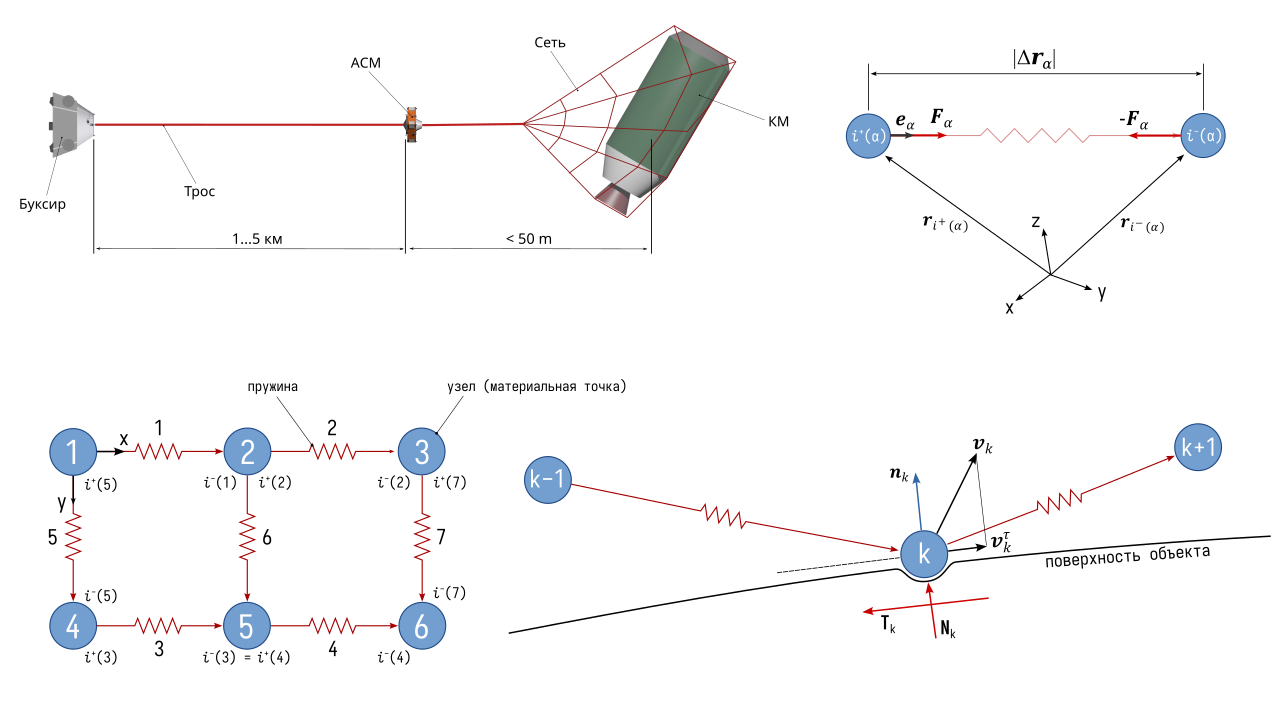
Структура сети
Для того, чтобы упростить запись уравнений движения сети, представляющей собой систему тел (материальных точек), опишем структуру связей этой системы, используя теорию графов.
Структура соединения узлов сети (материальных точек) может быть описана ориентированным графом. Вершины в этом графе представляют собой узлы сети (материальные точки), а соединяющие вершины дуги – это упругие элементы (пружины).
Ориентированный граф G(V,R) есть совокупность двух множеств — непустого множества V вершин и множества E упорядоченных пар различных элементов множества V (множество дуг или рёбер).
Структура ориентированного графа описывается матрицей инцидентности S c элементами \(S_{i\alpha}\). Количество строк матрицы S равно количество узлов сети (\(i=1,\ldots,n\)), а количество столбцов – количеству соединений между узлами (\(\alpha=1,\ldots,N\)), т.е. количеству пружин. Элемент матрицы инцидентности \(S_{i\alpha}\) равен +1, если дуга \(\alpha\) выходит из вершины i, минус 1, если дуга входит в вершину i и 0, если дуга не инцидентна вершине i.
Матрица инцидентности описывает не только связь узлов, но и направление этой связи, которое при записи уравнений движения двух смежных узлов позволяет задаться положительным направлением силы упругого взаимодействия между ними. Ниже на рисунке показан пример матрицы инцидентности для сети, состоящей из 6 узлов.
При записи уравнений движения также используются функции \(i^+(\alpha)\) и \(i^-(\alpha)\): функция \(i^+(\alpha)\) равна индексу вершины, из которой дуга α выходит, \(i^-(\alpha)\) равна индексу вершины, в которую дуга α входит.
Для удобства формирования списка координат узлов сети разместим их на равномерной сетке и поместим первый (левый верхний) узел в начало координат. Ось x этой системы координат направим в сторону второго узла (вправо), ось y в сторону четвертого узла (вниз).
Узлы сети пронумеруем “построчно” слева направо, а затем сверху вниз, как показано на рисунке выше. Также слева направо пронумеруем все пружины (дуги), направленные вдоль оси x, а затем пружины, направленные вдоль оси y. Дуги направим от узла с меньшим индексом к узлу с большим индексом.
Силы между узлами сети
В рассматриваемой модели узлы сети соединяются невесомыми пружинами, которые имитируют упругие свойства нитей, соединяющих узлы сети. Если расстояние между двумя узлами сети увеличивается больше некоторой заданной свободной длины этой пружины \(l_\alpha^0\), то между этими узлами начинает действовать сила упругости, зависящая от деформации пружины и, если учитывается демпфирующие свойства материала сети, скорости этой деформации. Если расстояние между узлами меньше \(l_\alpha^0\), то сила взаимодействия между этими узлами считается равной нулю.
Вектор, соединяющий пару узлов, модуль которого будет определять длину пружины c номером \(\alpha\), будет определяться выражением \[\Delta \mathbf{r}_\alpha = -\mathbf{r}_{i^+(\alpha)}+\mathbf{r}_{i^-(\alpha)}, \quad \alpha=1,\ldots,N\]
Вектор \(\Delta \mathbf{r}_\alpha\) направлен от узла с индексом \(i^+(\alpha)\) к узлу с индексом \(i^-(\alpha)\). Это выражение можно записать в более общем виде с использованием матрицы инцидентности: \[\Delta \mathbf{r}_\alpha = - \sum_{k=1}^n S_{k \alpha} \mathbf{r}_k, \quad \alpha=1,\ldots,N\]
Если все координатные столбцы узлов объединить в векторную матрицу столбец \[\Delta \mathbf r = \begin{bmatrix} \Delta \mathbf{r}_1 \\ \Delta \mathbf{r}_2 \\ \ldots \\ \Delta \mathbf{r}_N \\ \end{bmatrix},\]
то можно записать \[\Delta \mathbf{r} = - \mathbf{S}^T \mathbf{r}.\]
Зная \(\Delta \mathbf{r}_\alpha\) определим столбец единичных векторов, направленных от узла \(i^{+}(\alpha)\) к узлу \(i^{-}(\alpha)\): \[\mathbf{e}_\alpha = \frac{\Delta \mathbf{r}_\alpha}{|\Delta \mathbf{r}_\alpha|}, \quad \alpha=1,\ldots,N\]
Эти векторы будут определять направление силы упругости при растяжении пружины от узла \(i^{+}(\alpha)\) к узлу \(i^{-}(\alpha)\).
Cила, действующая на узел сети \(i^{+}(\alpha)\), будет зависеть от удлинения пружины и проекции скорости движения узла \(i^{-}(\alpha)\) относительно узла \(i^{+}(\alpha)\) на направление \(\mathbf{e}_\alpha\): \[\mathbf{F}_\alpha = \begin{cases} \mathbf{e}_\alpha [ (|\Delta \mathbf{r}_\alpha|-l_{\alpha}^0)k_s + V_\alpha^e k_d]& |\Delta \mathbf{r}_\alpha|>l_\alpha^0 \\ \mathbf{0} & |\Delta \mathbf{r}_\alpha| \leq l_\alpha^0 \end{cases}\]
где \(k_s\) – жесткость нити (пружины) сети, \(k_d\) – коэффициент демпфирования, учитывающий демпфирующие свойства материала сети.
Проекция скорости узла \(i^{-}(\alpha)\) относительно узла \(i^{+}(\alpha)\) на направление \(\mathbf{e}_\alpha\) определяется выражением: \[V_\alpha^e = \mathbf{e}_\alpha \cdot (\mathbf{v}_{i^-(\alpha)} -\mathbf{v}_{i^+(\alpha)} ), \quad \alpha=1,\ldots,N\]
или \[V_\alpha^e = - \mathbf{e}_\alpha \cdot \sum_{k=1}^n S_{k \alpha} \mathbf{v}_k, \quad \alpha=1,\ldots,N\]
Взаимодействие сети с объектом
Взаимодействие сети с объектом происходит в узлах сети, т.е. если узел касается поверхности объекта в точке этого контакта возникает совместная деформация узла сети и поверхности объекта, что приводит к возникновению нормальной к поверхности объекта силы реакции \(\mathbf{N}_k\) и силы трения \(\mathbf{T}_k\), направленной против скорости скольжения узла по поверхности \(\mathbf{v}_k^\tau\). Приведенные упругие свойства узла и поверхности определяются коэффициентом жесткости \(k_c\) и коэффициентом демпфирования \(k_{dc}\).
Для примера предположим, что объект космического мусора имеет форму сферы радиуса R центр которой расположен в точке, определяемой радиус-вектором \(\mathbf{r}_c\). Предположим также, что масса объекта космического мусора существенно больше массы сети, что позволяет считать, что объект остается неподвижным в процессе взаимодействия с сетью.
Расстояние от узла \(k\) до центра сферы определяется модулем вектора \(\rho_k = \mathbf{r}_k - \mathbf{r}_c\). Предположим, что взаимодействие узла сети со сферой начинается при \(\rho_k < R\) – в этот момент на узел начинает действовать нормальная сила: \[\mathbf{N}_{k} = \begin{cases} [(R - |\mathbf{\rho}_k|) k_c + v_{kn} k_{dc}] \mathbf{n}_k & |\mathbf{\rho}_k| < R \\ 0 & |\mathbf{\rho}_k| \geq R \\ \end{cases}\]
где \(\mathbf{n}_k\) – единичный вектор нормали к поверхности объекта в точке контакта.
Сила сухого трения \(T_k\) при скольжении узла по поверхности тела будет определяться выражением: \[\mathbf{T}_{k} = - N_{k} f_c \mathbf{e}_v^\tau\]
где \(f_c\) коэффициент трения, \(\mathbf{e}_v^\tau\) - единичный вектор направления касательной скорости \(\mathbf{v}_k^\tau\) \[\mathbf{v}_k^\tau = \mathbf{v}_k - \mathbf{n}_k (\mathbf{n}_k \cdot \mathbf{v}_k), \quad \mathbf{e}_v^\tau = \mathbf{v}_k^\tau / |\mathbf{v}_k^\tau|.\]
Уравнения движения
Таким образом, каждый узел сети движется под действием суммы упругих сил, действующих со стороны смежных узлов, и сил в точке контакта узла с объектом (нормальная сила и сила трения). В общем случае уравнение движения каждого узла сети имеет вид: \[m_k \ddot{\mathbf r}_k = \sum_{\alpha=1}^N \mathbf{S}_{k\alpha} \mathbf F_{\alpha} + \mathbf{N}_k + \mathbf{T}_{k} \quad k=1,\ldots,N\]
где \(m_k\) – масса узла.
Модель сети в Octave/MATLAB
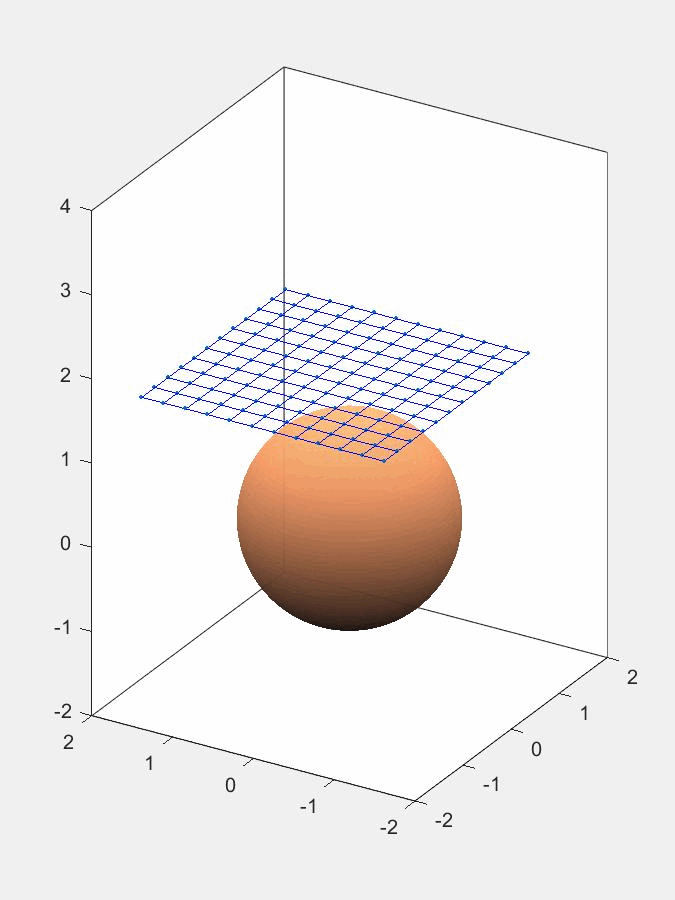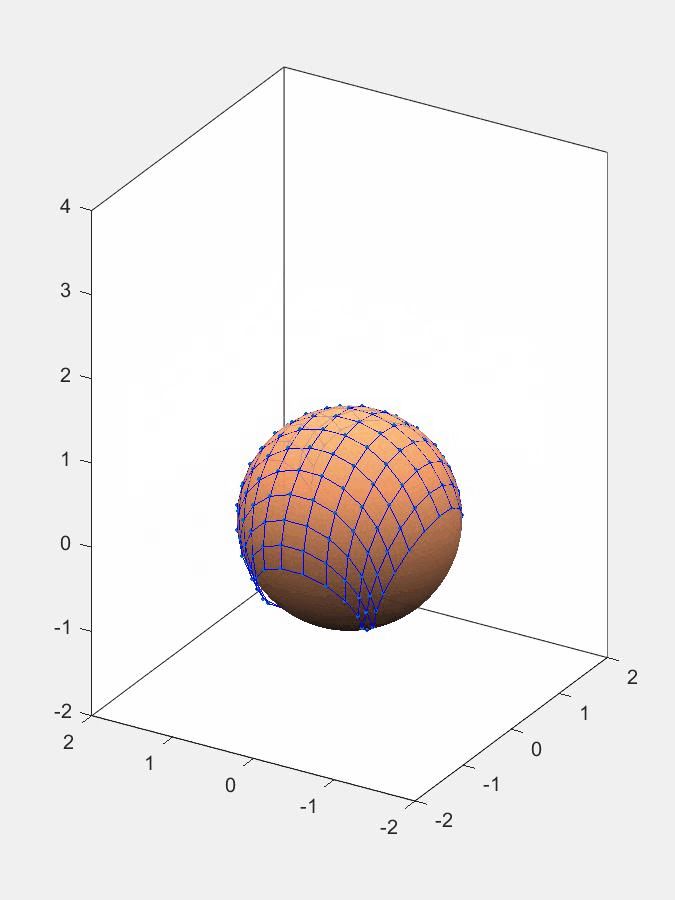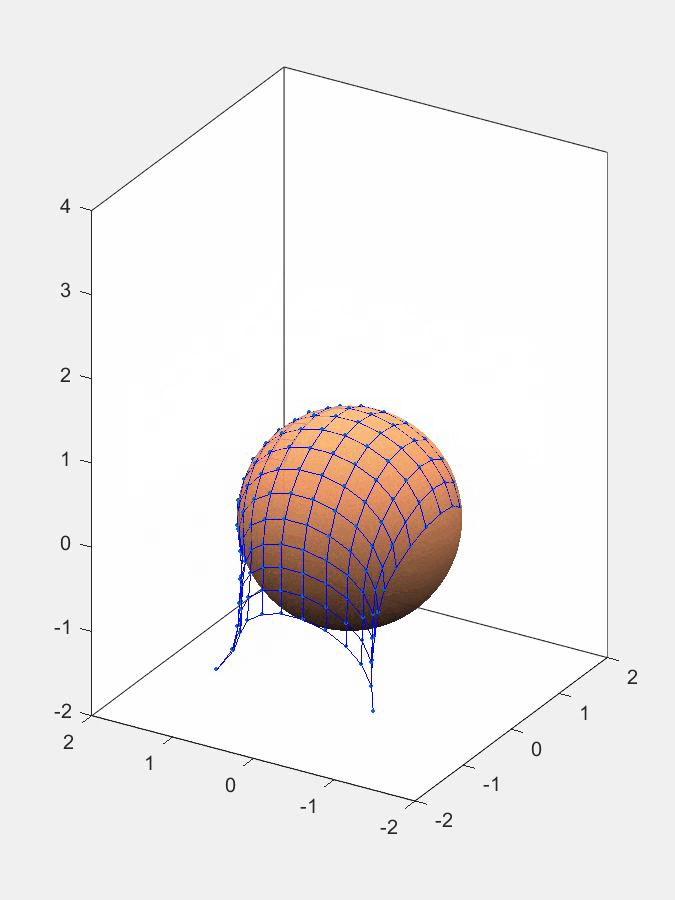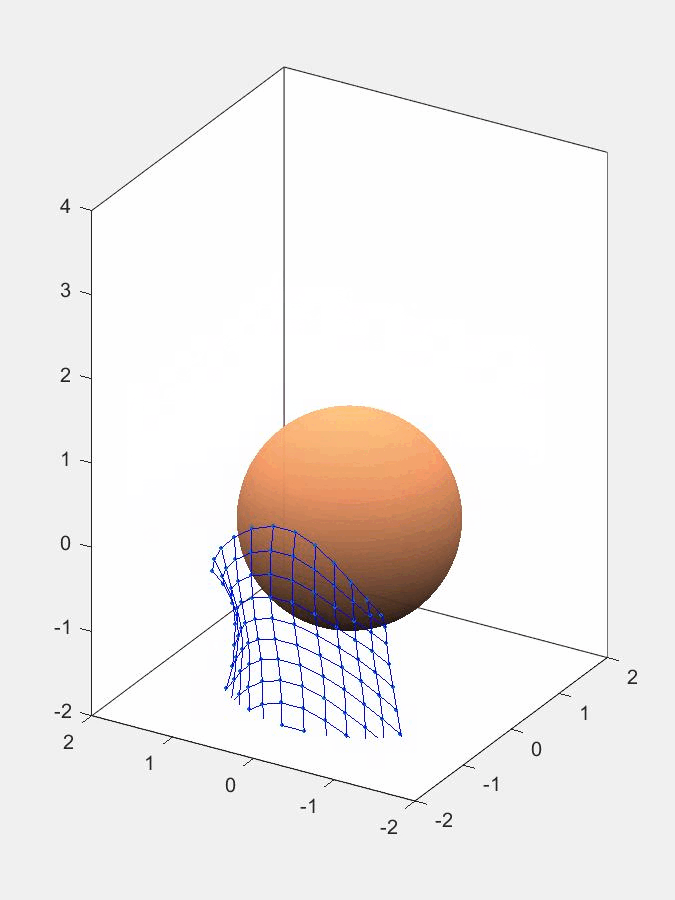
Для примера построим компьютерную модель взаимодействия сети с неподвижной сферой диаметром 1,2 м, которая расположена в начале координат. Сеть падет на сферу в однородном поле силы тяжести с ускорением 9,8 м/с\(^2\). В начальный момент времени сеть квадратной формы шириной 3 м находится на высоте 3 м (вдоль оси z) от начала координат.
Для построения модели создадим в MATLAB два файла: файл-функцию правых частей дифференциальных уравнений и файл-скрипт, в котором будут задаваться параметры системы, запускаться процесс интегрирования и выполняться анализ результатов.
Главный файл-скрипт
clc; clear all;
% Количество узлов
nc = 12; % в строке
nr = 12; % в столбце
% Размер сети
Lx = 3; Ly = 3;
n = nc*nr; % всего узлов
% Число дуг (связей, пружин)
na = 2*nc*nr-nc-nr;
% Матрица инцидентности
S = zeros(nc*nr,na);
Координаты узлов определим, используя функцию meshgrid, которая формирует матрицу (сеть) координат x,y,z узлов
% Координаты узлов (начальные)
[x,y,z] = meshgrid(linspace(0,Lx,nc),linspace(0,Ly,nr),1);
Например, для выражения [x,y,z] = meshgrid(1:2,1:3,1) x, y и z будут иметь вид: \[x = \begin{bmatrix} 1 & 2 \\ 1 & 2 \\ 1 & 2 \end{bmatrix}, \quad y = \begin{bmatrix} 1 & 1 \\ 2 & 2 \\ 3 & 3 \end{bmatrix}, \quad z = \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ 1 & 1 \end{bmatrix}.\]
% Матрица номеров узлов
nodes = reshape(1:n,nr,nc)';
% количество горизонтальных пружин
nar = (nc-1)*nr;
% количество вертикальных пружин
nac = (nr-1)*nc;
В следующей секции главного скрипта заполняется матрица инцидентности.
% по горизонтальным пружинам элементы i+
S(sub2ind(size(S), reshape(nodes(:,1:end-1)',1,[]) , 1:nar))= 1;
% по горизонтальным пружинам элементы i-
S(sub2ind(size(S), reshape(nodes(:,1:end-1)',1,[])+1, 1:nar))=-1;
% по вертикальным пружинам элементы i+
S(sub2ind(size(S), reshape(nodes(1:end-1,:),1,[]), nar+1:nar+nac))=1;
% по вертикальным пружинам элементы i-
S(sub2ind(size(S), reshape(nodes(1:end-1,:),1,[])+nc, nar+1:nar+nac))=-1;
% Начальные условия
r0 = [reshape(x',1,[]); reshape(y',1,[]); reshape(z',1,[])];
% Совмещаем центр сети с x = y = 0, z = 3;
rm = mean(r0,2); r0 = r0 - rm + [-0.3;0;3];
% Начальная скорость
v0 = zeros(3,n);
% Вектор начальных условий
q0 = [r0(:);v0(:)];
Заполняем структуру с параметрами системы, которая будет передаваться в функцию правых частей третьим аргументом.
% Структура для функции правых частей
p.n = nc*nr;
p.S = S;
% Масса узлов
p.m = ones(1,p.n)*0.1;
% Ускорение свободного падения
p.g = 9.81;
% Жесткость нитей
p.c = 1e3;
% Коэффициент демпфирования
p.d = 0.3e2;
% Свободная длина
p.l = x(1,2)-x(1,1);
% Радиус сферы, жесткость контакта
p.r = 1.2;
% Жесткость контакта сферы с узлом сети
p.cb = 1e5;
% Коэффициент демпфирования контакта сферы с узлом сети
p.db = 1e3;
Используем упрощенную модель сухого трения, при этом для исключения вычислительных проблем при скольжении узла по поверхности сферы со скоростью близкой к нулю, примем, что при скорости скольжения от 0 до 5 мм/с коэффициент трения линейно увеличивается до заданного значения p.fc = 0.2.
% Коэффициент трения при контакте сферы с узлом сети
p.fc = 0.2;
% Скорость скольжения, при которой к-т трения достигает
% максимума
p.vf = 0.005;
Запускаем процесс интегрирования и строим анимацию.
% Интегрирование
[t,q] = ode113(@(t,q) dqdt(t,q,p), 0:0.01:3.0, q0);
%% Анимация
h_nodes = plot3(r0(1,:),r0(2,:),r0(3,:),'.'); hold on;
h_lines = cell(na,1);
for i =1:na
XYZ = r0(:,abs(S(:,i))>0)';
h_lines{i} = line(XYZ(:,1),XYZ(:,2),XYZ(:,3),'Color','b');
end
[Xs,Ys,Zs] = sphere(64); colormap(copper);
hSurf = surf(Xs*p.r,Ys*p.r,Zs*p.r); shading flat;
c = hot(10);
set(hSurf,'FaceAlpha',0.8);
hold off;
xlim([-2,2]); ylim([-2,2]); zlim([-2,4]);
box on;
daspect([1,1,1]);
set(gcf,'Position',[100 100 1920 1080]);
%%
v = VideoWriter('net.avi'); open(v);
for k=1:size(t,1)
rk = reshape(q(k,1:3*p.n),3,[]);
h_nodes.XData = rk(1,:);
h_nodes.YData = rk(2,:);
h_nodes.ZData = rk(3,:);
for i =1:na
XYZ = rk(:,abs(S(:,i))>0)';
h_lines{i}.XData = XYZ(:,1);
h_lines{i}.YData = XYZ(:,2);
h_lines{i}.ZData = XYZ(:,3);
end
frame = getframe(gcf);
writeVideo(v,frame);
end
close(v);
Файл-функция правых частей
Далее приведена функция правых частей с построчными комментариями.
function dq = dqdt(t,q,p)
% Координатные столбцы узлов 3xn
r = reshape(q(1:3*p.n),3,[]);
% Координатные столбцы скоростей узлов 3xn
v = reshape(q(3*p.n+1:end),3,[]);
% n x 1 x 3 (координаты в 3 измерение: столбец векторов)
r3 = permute(r,[2,3,1]);
v3 = permute(v,[2,3,1]);
% --------------------------------------------------------------------
% Силы между узлами
% --------------------------------------------------------------------
% вектор от i+(a) к i-(a)
dr = permute(-pagemtimes(p.S',r3),[3,1,2]);
% расстояния между узлами
dist_nodes = sqrt(sum(dr.^2,1));
spring_deformation = dist_nodes>p.l;
% Упругая сила между узлами (если деформация положительная)
a_nodes = 0;
if any(spring_deformation)
% скорость i-(a) относительно i+(a)
dv = permute(-pagemtimes(p.S',v3),[3,1,2]);
% единичные вектора направления от i+(a) к i-(a)
dr_e = dr./dist_nodes;
% проекция относительной скорости на направление от i+(a) к i-(a)
dv_dist = dot(dv,dr_e);
Fnodes = spring_deformation.*dr_e.*(p.c*(dist_nodes-p.l)+p.d*dv_dist);
Fnodes3 = permute(Fnodes,[2,3,1]);
a_nodes = permute(pagemtimes(p.S,Fnodes3),[3,1,2])./p.m;
end
% --------------------------------------------------------------------
% Контакт со сферой с центром (0,0) и радиусом p.r
% --------------------------------------------------------------------
dist_to_0 = sqrt(sum(r.^2));
% Расстояние до поверхности сферы.
% Отрицательное, если узел оказался внутри сферы
dist_tp_sphere = dist_to_0-p.r;
is_contact = dist_tp_sphere<0;
a_contact = 0;
if any(is_contact)
% Вектор нормали в точке контакта
er = r./dist_to_0;
% Нормальная скорость
vr = dot(v,er);
% Нормальная сила
Nc = -is_contact.*(er.*(dist_tp_sphere*p.cb+vr.*p.db));
% Касательная скорость
vt = v-vr.*er;
% Модуль касательной скорости
vtm = sqrt(sum(vt.^2));
% Направление касательной скорости
et = vt./vtm;
% Если касательная скорость нулевая,
% то получившийся при делении nan заменяем на 0
et(isnan(et)) = 0;
% К-т трения функция скорости скольжения
fc = interp1([0;p.vf],[0;p.fc],vtm,"linear",p.fc);
% Вектор силы трения
Fc =-sqrt(sum(Nc.^2)).*fc.*et;
% Ускорение от контактной силы
a_contact = (Nc+Fc)./p.m;
end
% Гравитационное ускорение
ag = repmat([0;0;-p.g],1,p.n);
% Полное ускорение
a = a_nodes + ag + a_contact;
dq = [v(:); a(:)];
end
Результат работы программы