Кинематические уравнения.
Задание для лабораторной работы по курсу Динамика твёрдого тела и систем тел.
Задание 1
Разработайте функцию определения производной координат кватерниона по заданным координатам кватерниона (первый аргумент функции – столбец 4x1) и проекциям угловой скорости тела на связанные оси (второй аргумент функции – столбец 3x1):
function dquat = kinematic_Quat(quat, w)
...
end
Задание 2
Разработайте функцию определения производной элементов матрицы направляющих косинусов по заданной матрице направляющих косинусов (первый аргумент функции – матрица 3x3) и проекциям угловой скорости тела на связанные оси (второй аргумент функции – столбец 3x1):
function dA = kinematic_Matrix(A, w)
...
end
Задание 3
Угловое положение системы координат, связанной с твердым телом в начальный момент времени (\(t = 0\)) определяется тремя углами \(\alpha_1 = 10^o\), \(\alpha_2 = 30^o\) и \(\alpha_3 = 60^o\) (пассивная точка зрения). Последовательность поворотов определяется из таблицы:
| Вариант | Последовательность |
|---|---|
| 1 | 313 |
| 2 | 121 |
| 3 | 232 |
| 4 | 323 |
| 5 | 131 |
| 6 | 212 |
| 7 | 123 |
| 8 | 231 |
| 9 | 132 |
| 10 | 312 |
| 11 | 321 |
| 12 | 213 |
Номер варианта = 1 + (NNNNN mod 12), где NNNNN – номер зачетной книжки.
Проекции угловой скорости тела на связанные оси изменяются по закону: \[\omega_x = t \text{ рад/с}, \quad \omega_y = \cos (t/6) \text{ рад/с}, \quad \omega_z = \cos(t/5) \text{ рад/с}\]
Постройте графики изменения углов на интервале от 0 до 10 с.
Задание 4
Робот манипулятор состоит из трех звеньев, соединенных тремя шарнирами. Первый шарнир соединяет неподвижную опору и звено 1, второй шарнир звено 1 и звено 2 и третий шарнир звено 2 и звено 3. Каждый шарнир имеет одну степень свободы.
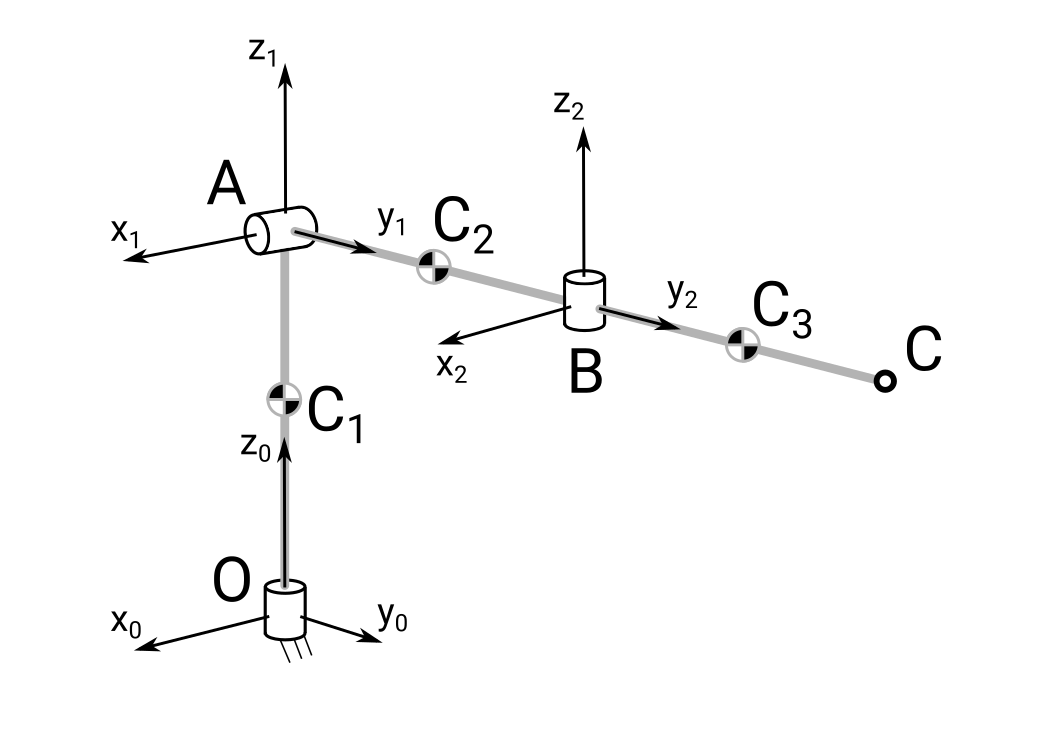 Вариант 1
Вариант 1
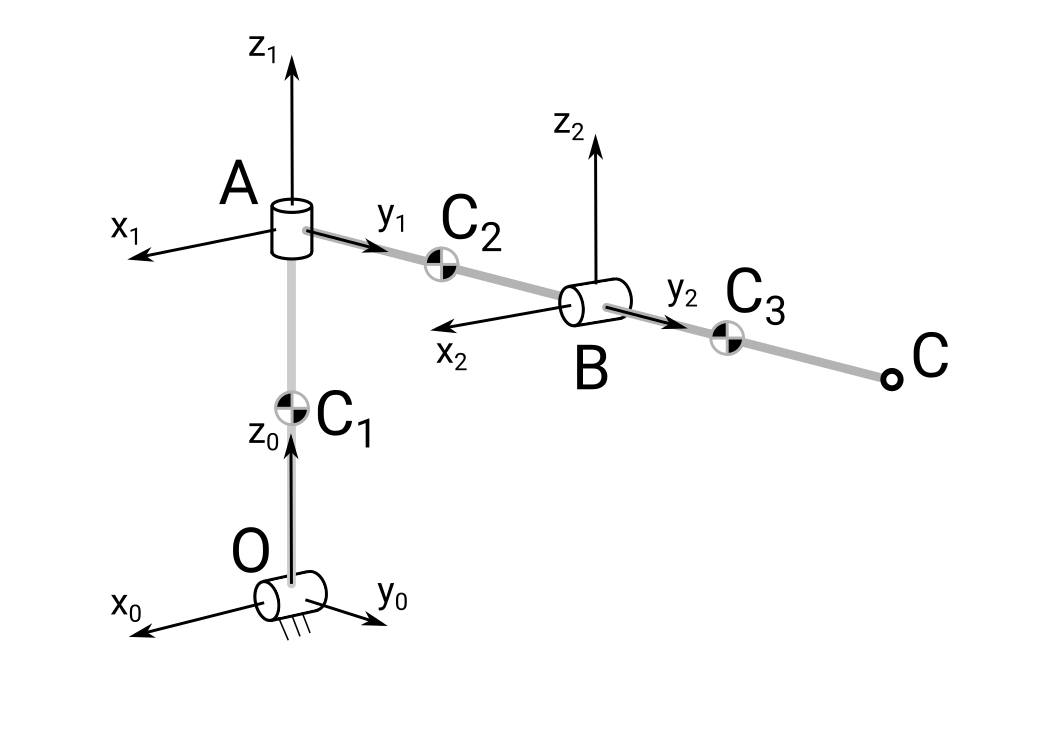 Вариант 2
Вариант 2
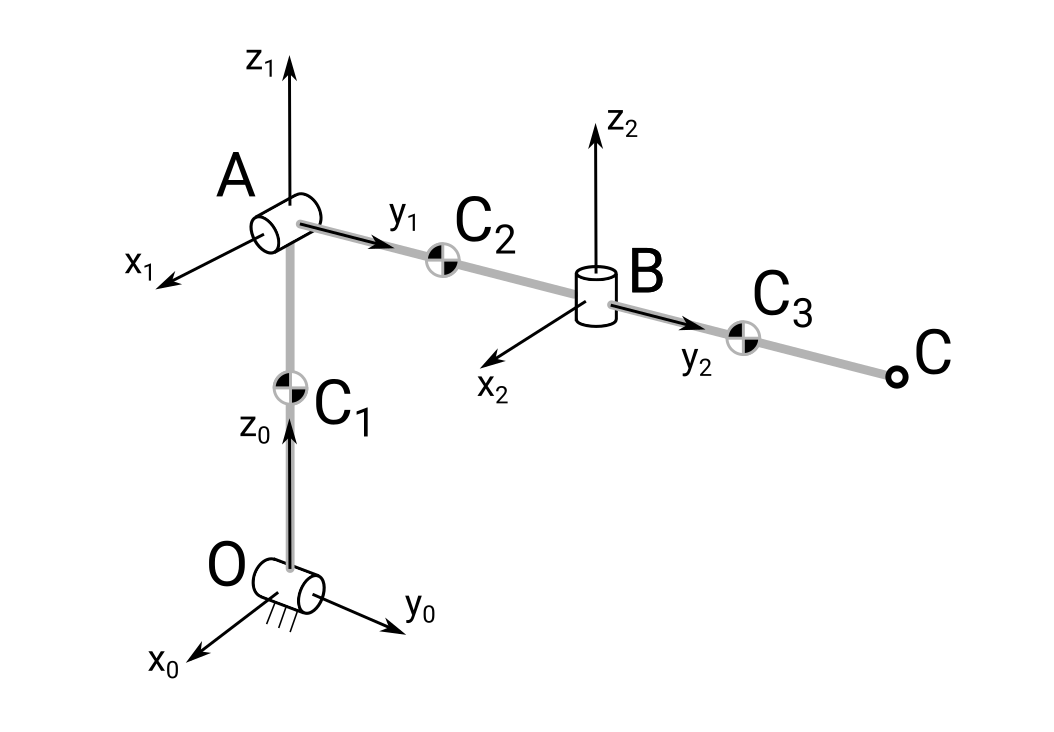 Вариант 3
Вариант 3
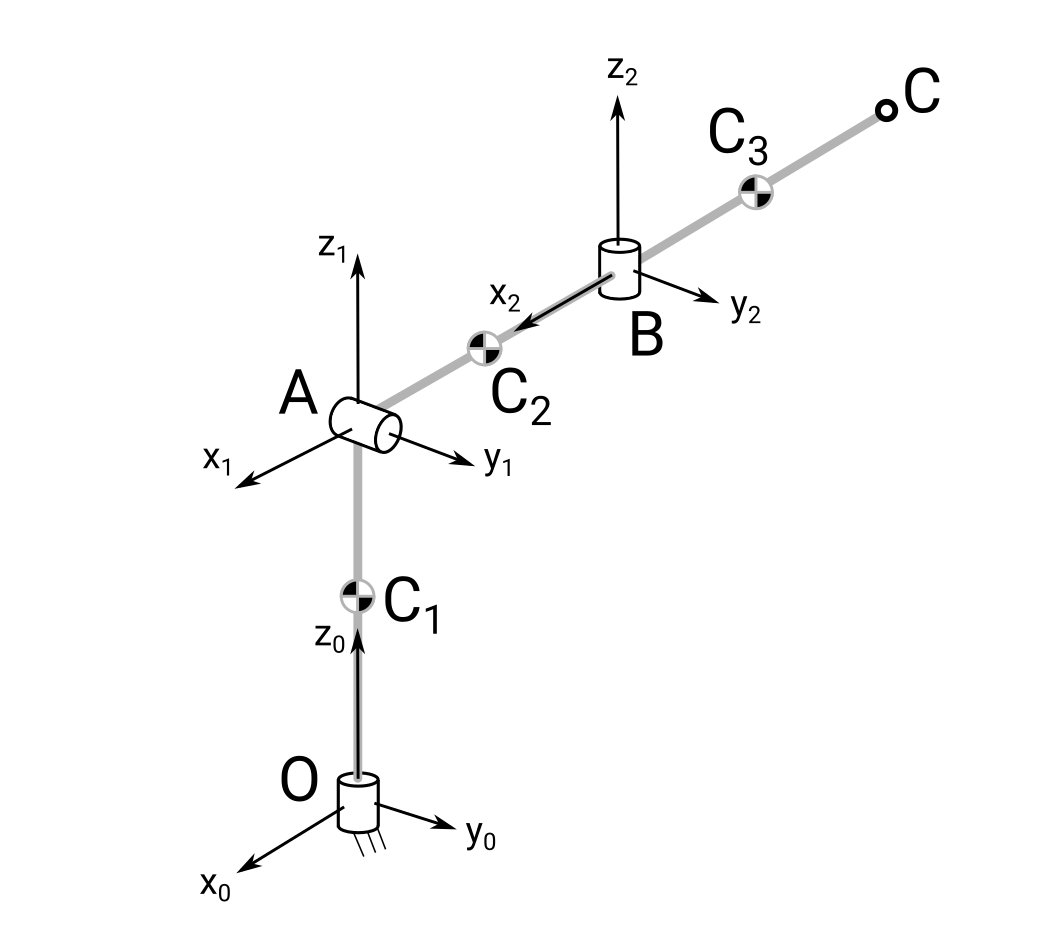 Вариант 4
Вариант 4
- Записать в матричном виде выражение для скорости точки С манипулятора.
- Вычислить координатный столбец скорости точки С манипулятора в момент времени когда:
Номер варианта определяется формулой: ВАРИАНТ = 1 + NNNNN mod 4. Длины всех звеньев равны 1 м: \[OA = AB = BC = 1\text{ м}.\]
Пример решения
На рисунке показан механизм, состоящий из четырёх звеньев, соединённых цилиндрическими шарнирами. Механизм имеет четыре степени свободы и его положение определяется четырьмя углами: \(\varphi_1\), \(\varphi_2\), \(\varphi_3\), \(\varphi_4\):
- угол \(\varphi_1\) определяет вращение звена 1 вокруг оси \(C_0 z_0\) неподвижной системы координат \(C_0x_0y_0z_0\), совпадающей по направлению с осью \(C_1 z_1\) системы координат \(C_1x_1y_1z_1\);
- звено 2 вращается вокруг оси \(С_1 y_1\) системы координат \(C_1x_1y_1z_1\), совпадающей по направлению с осью \(C_2 y_2\) системы координат \(C_2x_2y_2z_2\);
- звено 3 вращается вокруг оси \(x_2\) системы координат \(C_2x_2y_2z_2\), совпадающей по направлению с осью \(C_3 x_3\) системы координат \(C_3x_3y_3z_3\);
- звено 4 вращается вокруг оси \(z_3\) системы координат \(C_3x_3y_3z_3\), совпадающей по направлению с осью \(C_4 z_4\) системы координат \(C_4x_4y_4z_4\).
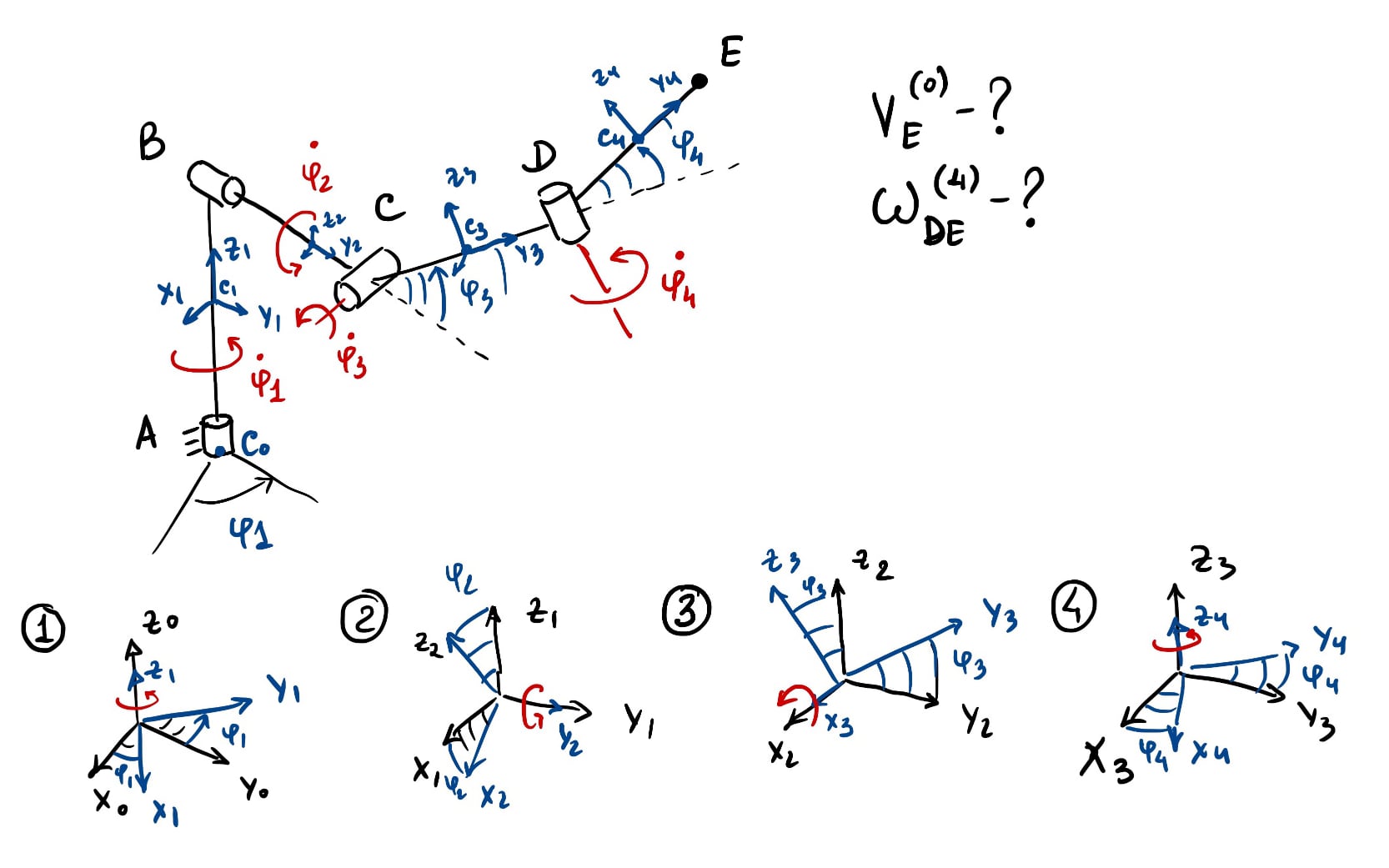 Схема механизма
Схема механизма
При \(\varphi_1=\varphi_2=\varphi_3=\varphi_4\) все системы координат, связанные со звеньями, совпадают с системой координат \(C_0x_0y_0z_0\).
- Найти координатный столбец вектора абсолютной скорости точки Е в базисе 0.
- Найти координатный столбец абсолютной угловой скорости звена 4 в базисе 4.
Координатный столбец вектора абсолютной скорости точки Е в базисе 0.
Введем следующие обозначения для радиус-векторов: \[{\vec{\rho}}_1=\vec{AB},\ \ {\vec{\rho}}_2=\vec{BC},\ \ {\vec{\rho}}_3=\vec{CD},\ \ {\vec{\rho}}_4=\vec{DE}.\]
Радиус-вектор точки Е относительно начала неподвижной системы координат \(C_0x_0y_0z_0\) определяется выражением: \[{\vec{r}}_E={\vec{\rho}}_1+{\vec{\rho}}_2+{\vec{\rho}}_3+{\vec{\rho}}_4.\]
Координатный столбец вектора \({\vec{r}}_E\) в базисе \(C_0x_0y_0z_0\): \[r_E^{(0)}=\rho_1^{(0)}+\rho_2^{(0)}+\rho_3^{(0)}+\rho_4^{(0)}=A^{01}\left(\rho_1^{\left(0\right)}+A^{12}\left(\rho_2^{\left(2\right)}+A^{23}\left(\rho_3^{\left(3\right)}+A^{34}\rho_4^{\left(4\right)}\right)\right)\right)\]
Производная координатного столбца \(r_E^{(0)}\) по времени представляет собой координатный столбец скорости точки \(Е\) в базисе 0: \[\frac{dr_E^{\left(0\right)}}{dt}=V_E^{(0)}={\dot{A}}^{01}\left(\rho_1^{\left(1\right)}+A^{12}\left(\rho_2^{\left(2\right)}+A^{23}\left(\rho_3^{\left(3\right)}+A^{34}\rho_4^{\left(4\right)}\right)\right)\right)+A^{01}\left({\dot{A}}^{12}\left(\rho_2^{\left(2\right)}+A^{23}\left(\rho_3^{\left(3\right)}+A^{34}\rho_4^{\left(4\right)}\right)\right)+A^{12}\left({\dot{A}}^{23}\left(\rho_3^{\left(3\right)}+A^{34}\rho_4^{\left(4\right)}\right)+A^{23}\left({\dot{A}}^{34}\rho_4^{\left(4\right)}\right)\right)\right).\]
Производные координатных столбцов \(\rho_1^{(1)}\), \(\rho_2^{(2)}\), \(\rho_3^{(3)}\), \(\rho_4^{(4)}\) равны нулю поскольку вектора, соответствующие этим координатным столбцам, движутся вместе с соответствующими базисами. Например, вектор \(\vec{\rho}_1\) вместе с базисом \(C_1 x_1 y_1 z_1\) вращается вокруг оси \(C_1 z_1\) и координаты вектора \(\vec{\rho}_1\) в этом базисе не меняются. Аналогично, вектор \(\vec{\rho}_2\) вращается вместе с базисом \(C_2 x_2 y_2 z_2\) вокруг оси \(C_2 y_1\) и координаты вектора \(\vec{\rho}_2\) в этом базисе не изменяются.
Введя обозначения \[\rho_{24}^{(2)}=\rho_2^{(2)}+A^{23} \rho_{34}^{(3)}, \quad \rho_{34}^{(3)}=\rho_3^{\left(3\right)}+A^{34}\rho_4^{\left(4\right)},\]
выражение для скорости точки Е можно упростить: \[V_E^{(0)}={\dot{A}}^{01}\left(\rho_1^{\left(1\right)}+A^{12}\rho_{24}^{(2)}\right)+A^{01}\left({\dot{A}}^{12}\rho_{24}^{(2)}+A^{12}\left({\dot{A}}^{23}\rho_{34}^{(3)}+A^{23}\left({\dot{A}}^{34}\rho_4^{\left(4\right)}\right)\right)\right).\]
С учетом выражений для производных матриц поворота: \[\dot{A}^{01} = A^{01} \widetilde{\Omega}_1^{(1)},\quad \dot{A}^{12} = A^{12} \widetilde{\Omega}_2^{(2)},\] \[\dot{A}^{23}=A^{23} \widetilde{\Omega}_3^{(3)},\quad \dot{A}^{34}=A^{34} \widetilde{\Omega}_4^{(4)}.\]
Матрица \(\widetilde{\Omega}_1^{(1)}\) – кососимметрическая матрица угловой скорости звена 1 относительно неподвижной системы координат, составленная из компонент координатного столбца вектора угловой скорости звена 1 относительно неподвижной системы координат: \[\Omega_1^{(1)}=\begin{bmatrix} \Omega_{1x} \\ \Omega_{1y} \\ \Omega_{1z} \end{bmatrix}\]
Кососимметрическая матрица \(\widetilde{\Omega}_1^{(1)}\) имеет вид: \[\widetilde{\Omega}_1^{(1)}=\begin{bmatrix} 0 & -\Omega_{1z} & \Omega_{1y} \\ \Omega_{1z} & 0 &-\Omega_{1x} \\ -\Omega_{1y} & \Omega_{1x} & 0 \end{bmatrix}\]
Учитывая, что звено 1 вращается вокруг оси \(z_1\) системы координат \(C_1x_1y_1z_1\): \[\widetilde{\Omega}_1^{(1)}= \begin{bmatrix} 0 & -\Omega_{1z} & 0 \\ \Omega_{1z} & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & -\dot{\varphi}_1 & 0 \\ \dot{\varphi}_1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\]
Матрица преобразования координат из базиса 1 в базис 0 при повороте вокруг оси \(z_0\ (z_1)\): \[A^{01}=\begin{bmatrix}\cos{\varphi_1}&-\sin{\varphi_1}&0\\\sin{\varphi_1}&\cos{\varphi_1}&0\\0&0&1\\\end{bmatrix}.\]
Матрица \({\widetilde{\Omega}}_2^{(2)}\) – кососимметрическая матрица угловой скорости звена 2 относительно звена 1, которая с учётом того, что звено 2 вращается вокруг оси \(C_1 y_1\) системы координат \(C_1x_1y_1z_1\) (совпадающей по направлению с осью \(C_2 y_2\)) определяется выражением: \[\widetilde{\Omega}_2^{(2)}= \begin{bmatrix} 0 & 0 & {\dot{\varphi}}_2 \\ 0 & 0 & 0\\ -{\dot{\varphi}}_2 & 0 & 0 \end{bmatrix}.\]
Матрица преобразования координат из базиса 2 в базис 1 при повороте вокруг оси \(C_1 y_1\ (C_2 y_2)\): \[A^{12}= \begin{bmatrix} \cos{\varphi_2} & 1 & \sin{\varphi_2}\\ 0 & 1 & 0\\ -\sin{\varphi_2} & 0 & \cos{\varphi_2} \\ \end{bmatrix}.\]
Матрица \(\widetilde{\Omega}_3^{(3)}\) – кососимметрическая матрица угловой скорости звена 3 относительно звена 2, которая с учётом того, что звено 3 вращается вокруг оси \(C_3 x_3\) системы координат \(C_3x_3y_3z_3\) (совпадающей по направлению с осью \(C_2 x_2\)) определяется выражением: \[\widetilde{\Omega}_3^{(3)}= \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -\dot{\varphi}_3 \\ 0 & \dot{\varphi}_3 & 0 \\ \end{bmatrix}.\]
Матрица преобразования координат из базиса 3 в базис 2 при повороте вокруг оси \(C_2 x_2\ (C_3 x_3)\): \[A^{32}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\varphi_3} & -\sin{\varphi_3} \\ 0 & \sin{\varphi_3} & \cos{\varphi_3} \\ \end{bmatrix}.\]
Матрица \(\widetilde{\Omega}_4^{(4)}\) – кососимметрическая матрица угловой скорости звена 4 относительно звена 3, которая с учётом того, что звено 4 вращается вокруг оси \({C_4z}_4\) системы координат \(C_4x_4y_4z_4\) (совпадающей по направлению с осью \(C_3z_3\)) определяется выражением: \[\widetilde{\Omega}_4^{(4)} = \begin{bmatrix} 0 & -{\dot{\varphi}}_4 & 0 \\ \dot{\varphi}_4 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}.\]
Матрица преобразования координат из базиса 4 в базис 3 при повороте вокруг оси \(C_4 z_4\): \[A^{34}=\begin{bmatrix} \cos{\varphi_4}&-\sin{\varphi_4}&0\\ \sin{\varphi_4}&\cos{\varphi_4}&0\\ 0&0&1 \end{bmatrix}.\]
Пример кода на языке MATLAB
% Оператор тильда
tilde = @(w) [0 -w(3) w(2); w(3) 0 -w(1); -w(2) w(1) 0];
% Матрица поворота вокруг оси x
Ax = @(a) [1 0 0; 0 cos(a) -sin(a); 0 sin(a) cos(a)];
% Матрица поворота вокруг оси y
Ay = @(a) [cos(a) 0 sin(a); 0 1 0; -sin(a) 0 cos(a)];
% Матрица поворота вокруг оси z
Az = @(a) [cos(a) -sin(a) 0; sin(a) cos(a) 0; 0 0 1];
% Исходные данные. Угол, производная угла
phi_1 = 1.0; dphi_1 = 1.0;
phi_2 = 1.5; dphi_2 = 1.5;
phi_3 = 0.5; dphi_3 = 0.5;
phi_4 = 1.0; dphi_4 = 1.0;
% Относительные угловые скорости
Omega1_in_1 = [0;0;dphi_1];
Omega2_in_2 = [0;dphi_2;0];
Omega3_in_3 = [dphi_3;0;0];
Omega4_in_4 = [0;0;dphi_4];
% Матрицы поворота
A01 = Az(phi_1);
A12 = Ay(phi_2);
A23 = Ax(phi_3);
A34 = Az(phi_4);
% Производные матриц поворота
dA01 = A01*tilde(Omega1_in_1);
dA12 = A12*tilde(Omega2_in_2);
dA23 = A23*tilde(Omega3_in_3);
dA34 = A34*tilde(Omega4_in_4);
% Координатные столбцы AB, BC, CD, DE
% в базисах 1, 2, 3 и 4 соответственно
AB = [0;0;1];
BC = [0;1;0];
CD = [0;1;0];
DE = [0;1;0];
%
CE_in_3 = CD + A34*DE;
BE_in_2 = BC + A23*CE_in_3;
% Абсолютная скорость точки Е в СК CoXoYoZo
VE = dA01*(AB+A12*BE_in_2) + A01*(dA12*BE_in_2+A12*(dA23*CE_in_3+A23*dA34*DE));
Координатный столбец абсолютной угловой скорости звена 4 в базисе 4.
Абсолютная угловая скорость звена DE определяется следующим образом: \[{\vec{\omega}}_{DE}={\vec{\omega}}_4={\vec{\Omega}}_1+{\vec{\Omega}}_2+{\vec{\Omega}}_3+{\vec{\Omega}}_4.\]
Координатный столбец вектора \({\vec{\omega}}_4\) в базисе \(C_4x_4y_4z_4\) будет определяться выражением \[\omega_4^{\left(4\right)}=\left(A^{34}\right)^T\left(A^{23}\right)^T\left(A^{12}\right)^T\Omega_1^{\left(1\right)}+\left(A^{34}\right)^T\left(A^{23}\right)^T\Omega_2^{\left(2\right)}+\left(A^{34}\right)^T\ \Omega_3^{\left(3\right)}+\Omega_4^{\left(4\right)}\]
Пример кода на языке MATLAB
w4_in_4 = A34'*(A23'*(A12'*Omega1_in_1+Omega2_in_2)+Omega3_in_3)+Omega4_in_4;
