Отделение группы космических аппаратов. Метод Монте-Карло
Условия
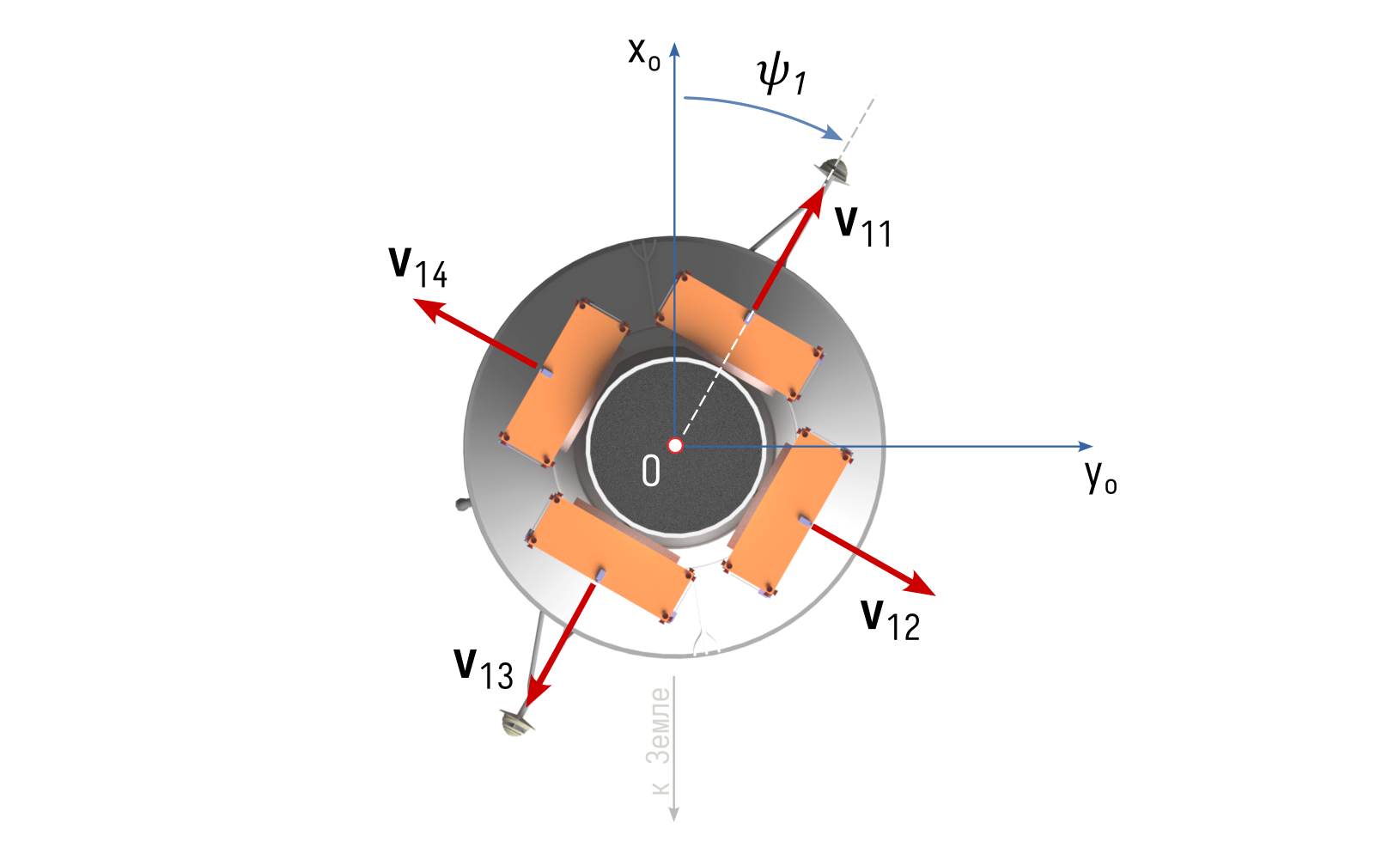
- От разгонного блока (РБ) на круговой орбите высотой \(h\) отделяются 12 космических аппаратов (КА).
- КА отделяются тремя группами с интервалом \(\Delta T\) между каждой группой; в каждой группе одновременно отделяются по 4 КА, которые расположены в одном поясе адаптера РБ.
- КА отделяются в плоскости орбиты; при отделении КА продольна ось РБ ориентирована вдоль оси \(Oz_o\) орбитальной подвижной системы координат РБ.
Орбитальная система координат (ОСК) движется с РБ и её начало совпадает с центром масс РБ. \(Ox_o\) направлена вдоль радиус-вектора РБ относительно центра масс Земли в направлении от Земли, ось \(Oy_o\) лежит в плоскости орбиты и направлена в сторону движения РБ по орбите, ось \(Oz_o\) дополняет систему координат до правой.

- Скорость отделения каждого КА (\(v_{ij}\)) – нормально-распределенная случайная величина с заданным средним значением \(V_s\) и стандартным отклонением равным 1 % от среднего значения.
- Средние значения скорости отделения для всех КА одинаковы.
- Перед отделением каждой группы выполняется разворот разгонного блока в плоскости орбиты на угол \(\psi_i\) в орбитальной системе координат, где \(i\) - номер группы.
Задание
- Определите углы разворота разгонного блока \(\psi_i\) (\(i=1,2,3\)) перед отделением каждой группы КА, при которых обеспечивается минимальная вероятность сближения КА на расстояние менее 50 м при этом исключается сближение КА и разгонного блока на расстояние менее 50 м в течение двух орбитальных периодов РБ.
- При выбранных углах разворота оцените частоту сближения любой пары КА на расстояние менее 100 м в течение двух орбитальных периодов РБ.
- При выбранных углах разворота определите верхнюю границу доверительного интервала вероятности сближения КА на расстояние меньше 100 м для доверительной вероятности 0,95.
Варианты заданий (номер варианта соответствует номеру в ведомости)
| Вариант | \(V_s\), м/с | \(\Delta T\), мин | h, км |
|---|---|---|---|
| 1 | 0.3 | 1 | 350 |
| 2 | 0.3 | 2 | 400 |
| 3 | 0.3 | 3 | 350 |
| 4 | 0.3 | 4 | 400 |
| 5 | 0.3 | 5 | 450 |
| 6 | 0.5 | 1 | 500 |
| 7 | 0.5 | 2 | 550 |
| 8 | 0.5 | 3 | 600 |
| 9 | 0.5 | 4 | 350 |
| 10 | 0.6 | 1 | 450 |
| 11 | 0.6 | 2 | 300 |
| 12 | 0.6 | 3 | 350 |
| 13 | 0.6 | 4 | 300 |
| 14 | 0.8 | 1 | 400 |
| 15 | 0.8 | 2 | 500 |
| 16 | 0.8 | 3 | 600 |
| 17 | 0.8 | 4 | 650 |
Методические рекомендации
КА и РБ рассматривать как материальные точки, движущиеся в центральном гравитационном поле.
Для анализа движения КА использовать линейные уравнения относительного орбитального движения КА (движения КА относительно РБ). Пример кода на языке MATLAB.
Для оценки вероятности сближения двух КА на расстояние менее заданного использовать метод Монте-Карло, выполняя серию 1000 расчётов и разыгрывая перед каждым расчётом скорость отделения КА при помощи генератора случайных чисел в соответствии с п. 4 условий.
Для определения верхней границы вероятности сближения любой пары КА на расстояние менее 100 м при заданной доверительной вероятности \(\beta\) необходимо определить оценить частоту \(p\) этого события:
где k – количество расчётов, в которых зарегистрировано сближение КА на расстояние менее 100 м, n=1000 – общее количество расчётов.
- Верхняя граница доверительного интервала вероятности этого события (\(\hat{p}\)) для доверительной вероятности \(\beta\) определяется решением уравнения [Вентцель Е. С., 1969]:
См. также Binomial proportion confidence interval
Определение доверительного интервала вероятности события по наблюдаемой частоте события в python
import statsmodels.api as sm
# Количество опытов
n = 1000
# Доверительная вероятность
b = 0.95
# Если событие в n опытах не произошло ни разу (count = 0)
sm.stats.proportion_confint(count=0, nobs=n, alpha=1-b, method="binom_test")
>> (0.0, 0.0038817608616778985)
# нижняя граница вероятности события равна 0
# верхняя граница 0,00388
# Если событие в n опытах произошло 1 раз (count = 1)
sm.stats.proportion_confint(count=1, nobs=n, alpha=1-b, method="binom_test")
>> (5.1291978908843065e-05, 0.005871787271765959)
# нижняя граница вероятности события 5,1e-5
# верхняя граница 0,00587
