NumPy. Векторы и матрицы

Движение наноспутника относительно станции определяется в орбитальной системе координат, движущейся вместе с орбитальной станцией по круговой орбите. Начало координат расположено в центре масс станции. Ось \(x_o\) орбитальной подвижной системы координат направлена от Земли вдоль радиус вектора станции. Ось \(y_o\) лежит в плоскости орбиты и направлена в сторону орбитальной скорости станции. Ось \(z_o\) дополняет систему координат до правой.

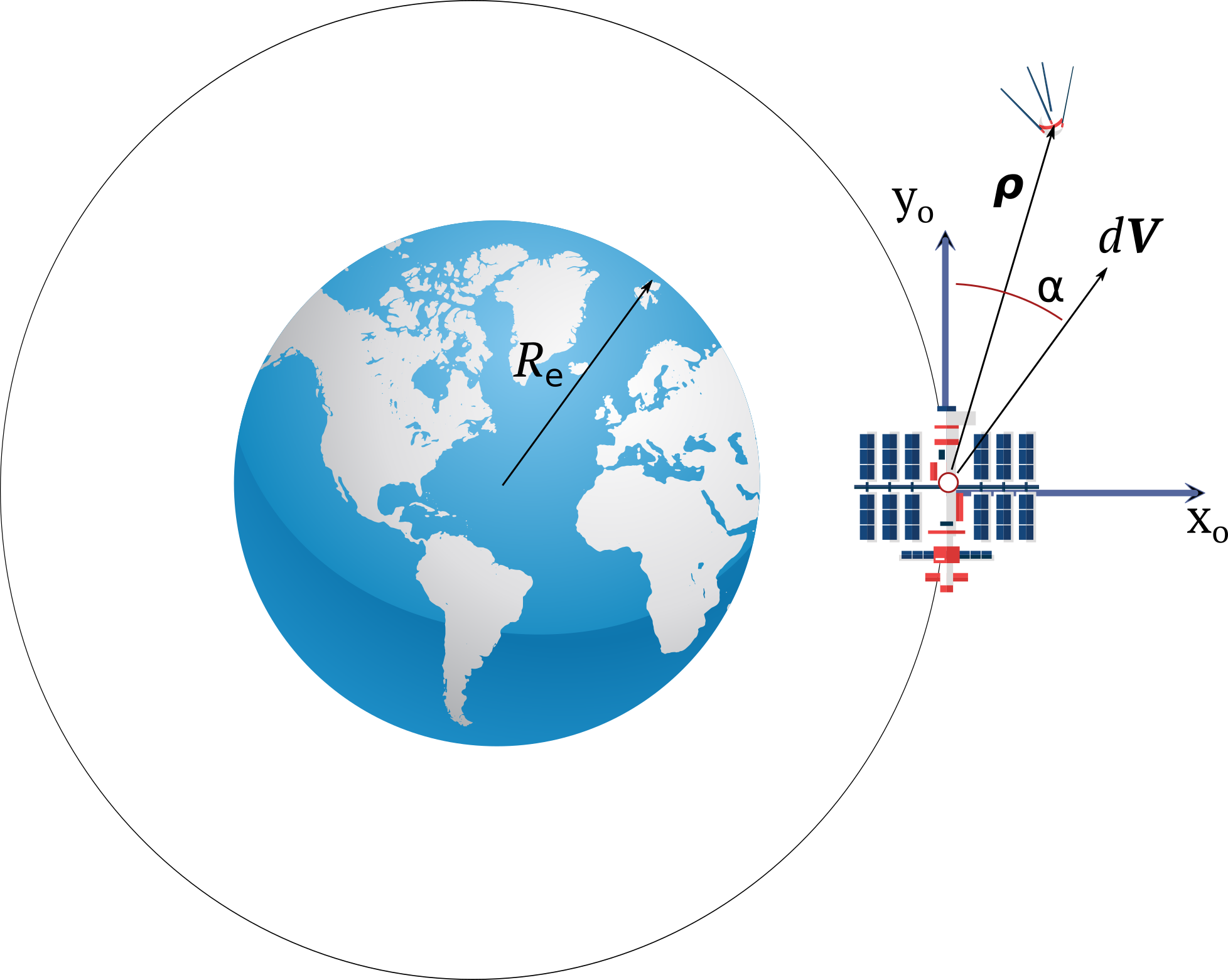
При отделении от станции с относительной скоростью \(V_0 = [\dot{x}_0, \dot{y}_0, \dot{z}_0]\) закон движения наноспутника в координатной форме имеет вид: \[\begin{aligned} & x(t) = \frac{1}{n} \left[ \dot{x}_0 \sin n t + 2 \dot{y}_0 (1-\cos nt) \right] \\ & y(t) = \frac{1}{n} \left[ 2 \dot{x}_0 ( \cos nt - 1) + \dot{y}_0 (4\sin nt - 3nt) \right] \\ & z(t) = \frac{\dot{z}_0}{n} \sin nt \end{aligned}\]

где \(n = 2\pi/T\) – угловая скорость орбитального движения станции, \(T\) – орбитальный период станции.

Создать функцию определения положения спутника относительно орбитальной подвижной системы координат, связанной со станцией, в моменты времени, заданные массивом t_array:

def rho(t_array):
    ...
    ...
    ...
    return res

Функция rho должна возвращать массив (numpy.array) \(n \times 4\), где n - количество элементов в массиве моментов времени t_array. Первый столбец результата – время (копия массива t_array), второй, третий и четвертый столбцы – значения координат \(x, y, z\) наноспутника относительно станции.

• Постройте траекторию движения спутника на интервале трёх орбитальных периодов станции, движущейся по круговой орбите высотой 400 км.
• Постройте график изменения расстояния между спутником и станцией на интервале трёх орбитальных периодов при начальной скорости отделения наноспутника

• Постройте график изменения расстояния между наноспутником и станцией.
• Определите расстояние и время минимального сближение наноспутника со станцией после его отделения (локальный экстремум - минимум) на интервале 3 орбитальных периодов. Алгоритм определения минимального расстояния должен работать для любого массива расстояний. В случае отсутствия локального минимума, если функция изменения расстояния монотонно возрастает, алгоритм должен возвращать numpy.Inf (бесконечность). Проверить работу алгоритма для различных начальных условий движения наноспутника. Оформите алгоритм в виде функции

def min_dist(t_d_array):
    # t_d_array - массив n*2
    # время, расстояние 
    ...
    ...
    ...
    return (t_min,d_min)