Углы Эйлера

Положение начала системы координат \(O_1 x_1 y_1 z_1\) относительно системы координат \(O_0 x_0 y_0 z_0\) определяется радиус-вектором \(\vec {r}_1\). Координатный столбец вектора \(\vec {r}_1\) в базисе \(O_0 x_0 y_0 z_0\): \[r_1^{(0)} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\]

Ориентация базиса \(O_1 x_1 y_1 z_1\) по отношению к базису \(O_0 x_0 y_0 z_0\) определяется тремя углами Эйлера (последовательность поворотов ZX’Z’’): \[\psi = 30 + (\text{NNNNN} \mod 30), \quad \theta = 60 + (\text{NNNNN} \mod 30), \quad \varphi = 10 + (\text{NNNNN} \mod 30)\]

где NNNNN - последние пять цифр номера зачетной книжки.

Положение точки А в базисе \(O_1 x_1 y_1 z_1\) определятся координатным столбцом \[\rho_A^{(1)} = \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix}\]

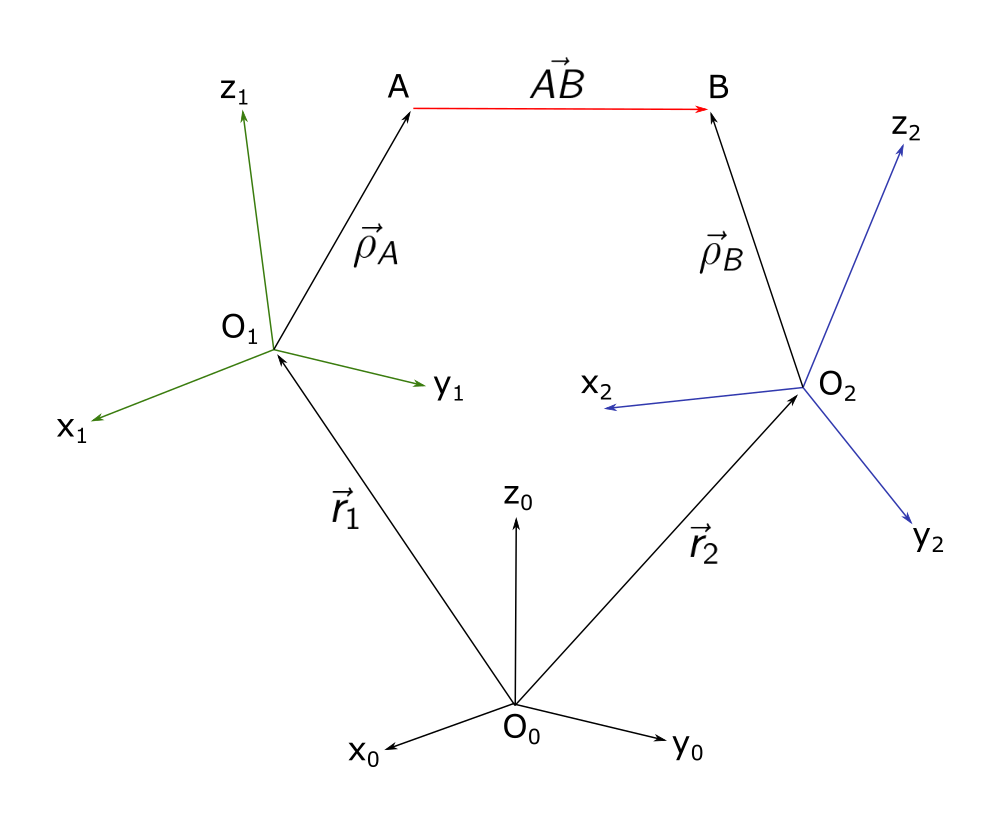
Положение начала системы координат \(O_2 x_2 y_2 z_2\) относительно системы координат \(O_0 x_0 y_0 z_0\) определяется радиус-вектором \(\vec {r}_2\). Координатный столбец вектора \(\vec {r}_2\) в базисе \(O_0 x_0 y_0 z_0\): \[r_2^{(0)} = \begin{bmatrix} -2 \\ 3 \\ 1 \end{bmatrix}\]

Ориентация базиса \(O_2 x_2 y_2 z_2\) по отношению к базису \(O_0 x_0 y_0 z_0\) определяется тремя углами Эйлера (последовательность поворотов XY’Z’’): \[\alpha_1 = 20 + (\text{NNNNN} \mod 30), \quad \alpha_2 = 30 + (\text{NNNNN} \mod 30), \quad \alpha_3 = 40 + (\text{NNNNN} \mod 30)\]

Положение точки А в базисе \(O_2 x_2 y_2 z_2\) определятся координатным столбцом \[\rho_A^{(1)} = \begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix}\]

1. Найти модуль вектора \(\vec{AB}\).
2. Найти координаты вектора \(\vec{AB}\) в базисе \(O_1 x_1 y_1 z_1\).
3. Найти координаты вектора \(\vec{AB}\) в базисе \(O_2 x_2 y_2 z_2\).