Орбитальное движение.

Разработать программу численного интегрирования движения материальной точки в центральном гравитационном поле Земли в геоцентрической инерциальной системе координат \(O X_0 Y_0 Z_0\).

Разработать функцию преобразования четырёх элементов орбиты спутника (\(\Omega, i, \omega, \vartheta\)) в декартовы координаты геоцентрической инерциальной системы координат \(O X_0 Y_0 Z_0\).

Разработать функцию вычисления матрицы преобразования координат из перигейной системы координат \(p x_p y_p z_p\) в геоцентрическую инерциальную систему \(O X_0 Y_0 Z_0\).

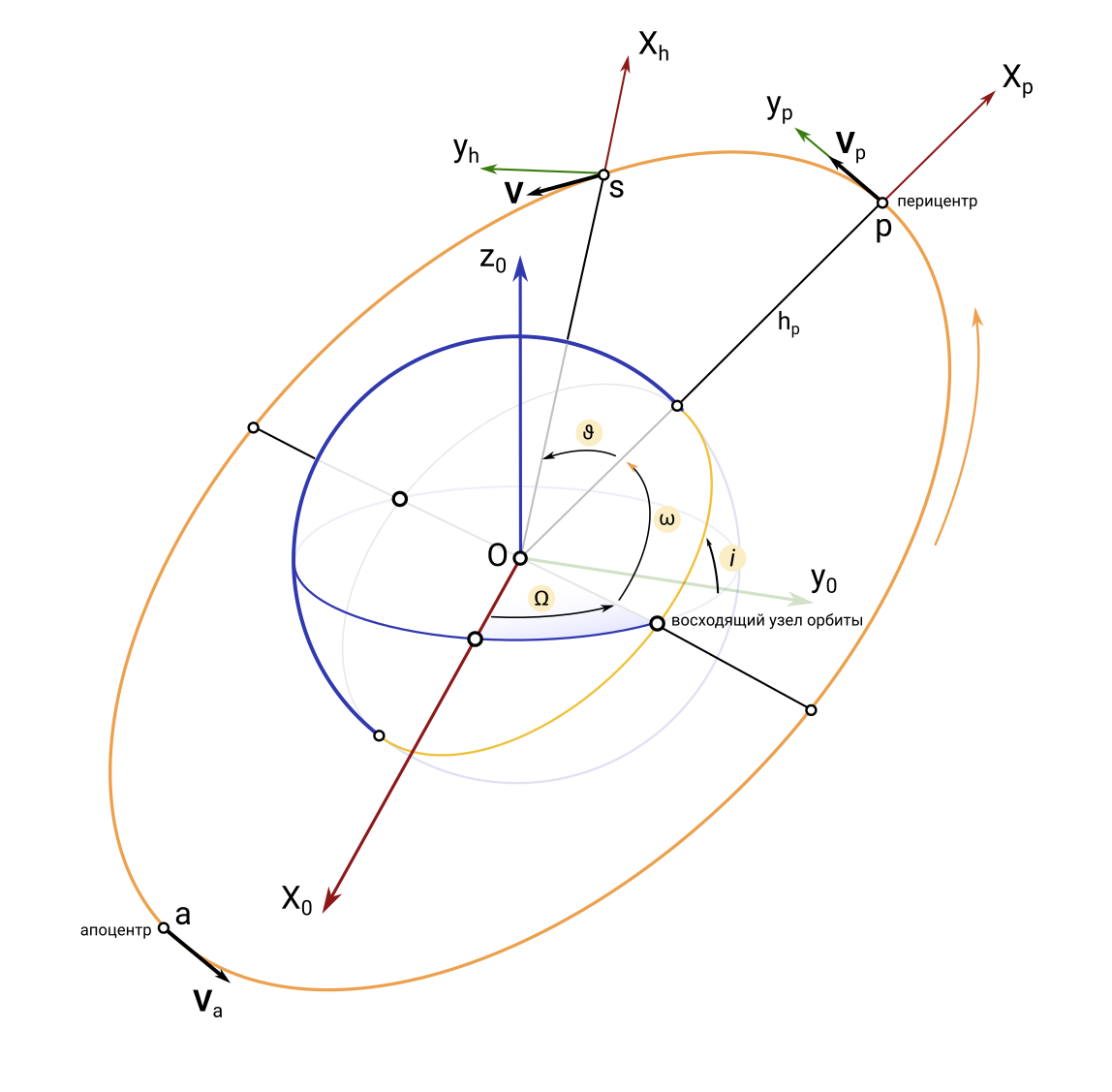
Ось \(x_p\) перигейной системы направлена из центра Земли в точку перигея орбиты, ось \(y_p\) лежит в плоскости орбиты и направлена в сторону орбитального движения КА, ось \(z_p\) дополняет систему до правой (перпендикулярная плоскости орбиты).

Проинтегрировать движение спутника для следующих начальных условий:

• Высота перигея, \(h_p\) = 200 км;
• Высота апогея, \(h_a\) = 200 + 50*(NNNNN mod 5) км;
• Долгота восходящего узла, \(\Omega\) = 10*(NNNNN mod 35) градус;
• Наклонение, \(i\) = 10 + (NNNNN mod 80) градус;
• Аргумент перицентра, \(\omega\) = 5 + 10*(NNNNN mod 35) градус;
• Угол истинной аномалии, \(\vartheta\) = 0 (спутник находится в точке перицентра).

где NNNNN – последние пять цифр зачетной книжки, a mod b - остаток от деления a на b. Например, для зачетной книжки 2017-00521 начальные условия буду вычисляться следующим образом:

• \(h_p\) = 200 км;
• \(h_a\) = 200 + 50(521 mod 5) = 200 + 50(1) = 250 км;
• \(\Omega\) = 10(521 mod 35) = 10(31) = 310 градусов;
• \(i\) = 10 (521 mod 80) = 10 + 41 = 51 градус;
• \(\omega\) = 5 + 10 (521 mod 35) = 5 + 10*31 = 315 градус.

Высота перигея и апогея позволят вычислить модуль начальной скорости спутника (в точке апоцентра). Остальные параметры орбиты позволят определить направление вектора начальной скорости.

Решение найти на интервале двух орбитальных периодов (T). Таблица решения должна содержать 240 точек на интервале от 0 до 2*Т.

В точке перицентра от спутника №1 отделяется спутник №2 с относительной скоростью 2 м/с в направлении орбитальной скорости. Найти решение для второго спутника. Найти численное решение на интервале двух орбитальных периодов спутника №1. Таблица решения должна содержать 240 точек на интервале от 0 до 2*Т.

Построить траекторию движения спутника №2 относительно спутника №1 в орбитальной системе координат спутника №1 в плоскости его орбиты.

Начало орбитальной подвижной системы координат совпадает с центром масс спутника. Ось \(S x_h\) орбитальной подвижной системы координат направлена из центра масс спутника от Земли параллельно радиус-вектору спутника относительно центра Земли, ось \(S y_h\) лежит в плоскости орбиты и направлена в сторону орбитального движения спутника, ось \(z_h\) дополняет систему до правой (перпендикулярная плоскости орбиты).

Методические указания

Эксцентрисистет орбиты (характеризует “вытянутость” орбиты): \[e = \frac{r_a-r_p}{r_p+r_a}\]

где \(r_p = R_e + h_p\) - расстояние от центра Земли до точки перигея, \(r_a = R_e + h_a\) - расстояние от центра Земли до точки апогея, \(R_e\) - средний радиус Земли.

Фокальный параметр орбиты \[p = \frac{r_p+r_a}{2} (1-e^2)\]

Скорость спутника в перигее \[V_p = \sqrt{\frac{\mu}{p}}(1+e)\]

Скорость спутника в апогее \[V_p = \sqrt{\frac{\mu}{p}}(1-e)\]

где \(\mu\) - гравитационный параметр Земли, равный произведению её массы на гравитационную постоянную: \(\mu = 398600.433\cdot 10^9\) м\(^3\)/c\(^2\).

Пример функция правых частей

function dq = dqdt(t,q,p)    
    % Координатный столбец радиус-вектора спутника
    r  = q(1:3);    
    % Координатный столбец скорости 
    v  = q(4:6);    
    % Гравитационный параметр
    mu = p.mu;
    % Координатный столбец ускорения спутника 
    a  = - mu*r/norm(r)^3;    
    dq = [v; a];
end

Файл-скрипт, запускающий процесс интегрирования

p.mu    = ...

ha      = ...;
hp      = ...;

% Долгота восходящего узла
RAAN    = ...; 
% Аргумент перигея
ap      = ...;

% Координатный столбец вектора начального положения и скорости спутника
r0      = ...
v0      = ...

% Период обращения
T       = ...  
tspan   = linspace(0,T,240);

q0      = [r0;v0];

opt     = odeset('RelTol', 1e-8);

[t, q]  = ode113(@(t,q,p), tspan, q0, opt);

...