Движение твердого тела под действием следящей силы

Задание для лабораторной работы по курсу Динамика твёрдого тела и систем тел.

Построить модель движения орбитальной ступени ракеты-носителя после отделения полезного груза в течение 30 секунд относительно орбитальной подвижной системы координат, которая считается инерциальной. Принять допущение о том, что орбитальная ступень движется только под действием силы тяги \(P\) сопла торможения.

Описание механической системы

  • Схема орбитальной ступени показана на рисунке 1.

Рисунок 1 – Схема ступени

  • Инерционно-массовые характеристики ступени
ПараметрЗначение
Масса ступени5000 кг
Положение центра масс, \(x_c\)3 м
Момент инерции относительно продольной оси5000 кг\(\cdot\)м \(^2\)
Момент инерции относительно любой поперечной оси10000 кг\(\cdot\)м \(^2\)
  • Тяга реактивного сопла увода

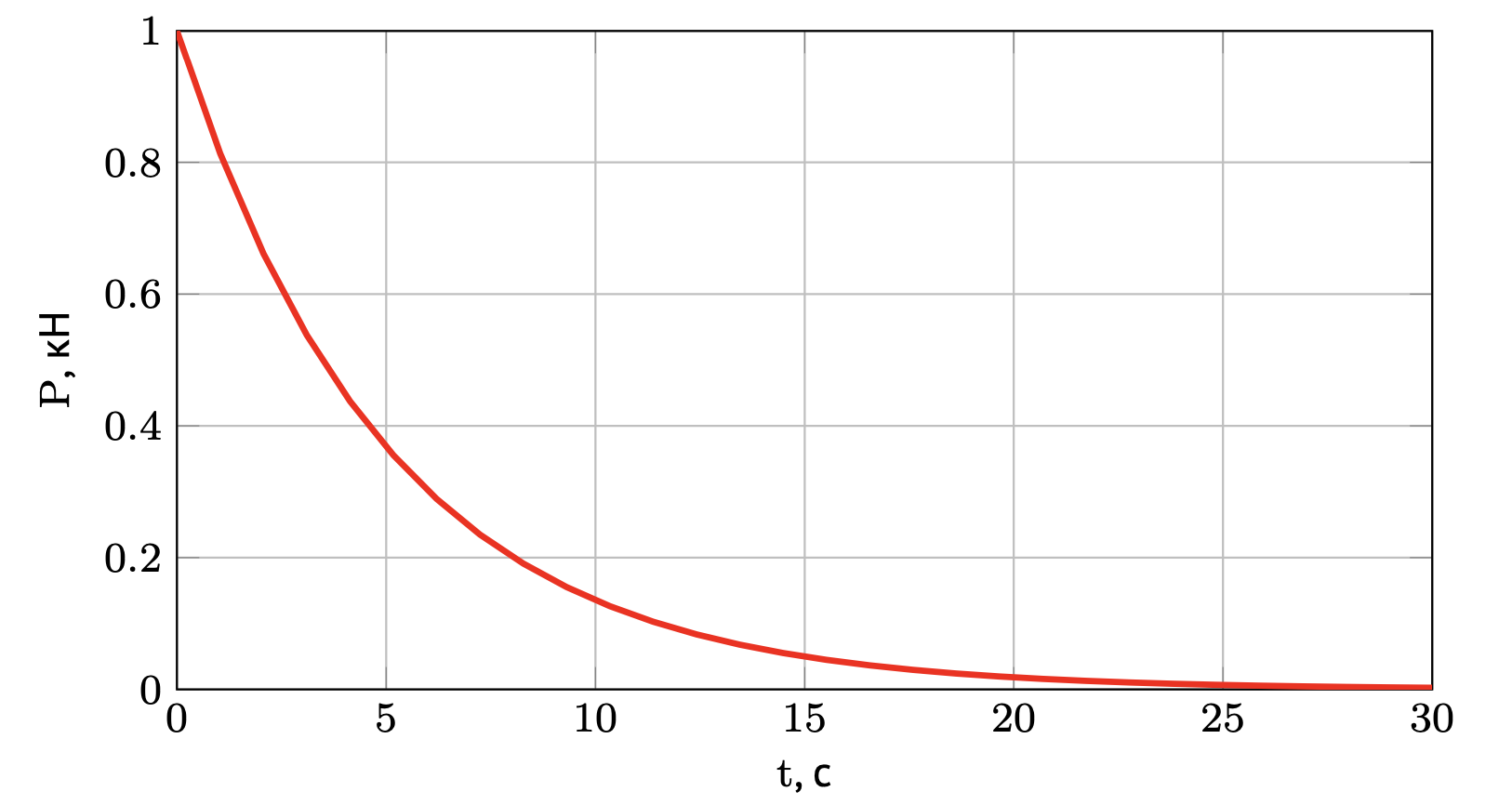Рисунок 2 – Закон изменения тяги реактивного сопла

В качестве параметров, определяющих угловое положение ступени, использовать

  • направляющие косинусы;
  • углы Эйлера (пассивная точка зрения);
  • кватернионы

Последовательность поворотов углов Эйлера выбирается из следующей таблицы:

ВариантПоследовательность
1313
2231
3121
4312
5132
6321
7213
8232
9323
10131
11212

Номер варианта определяется по номеру в ведомости.

  • Начальные условия

В начальный момент времени координаты центра масс равны нулю, скорость ступени равна нулю (по отношению к орбитальной подвижной системы координат). Начальные углы поворота определяются выражением: \[\varphi_1 = 1 + (\text{N} \times 100) \mod 5, \; \varphi_1 = (\text{N} \times 100) \mod 10, \; \varphi_1 = (\text{N} \times 100) \mod 15.\]

где \(N\) – номер варианта.

Проекция начальной угловой скорости ступени на ее продольную ось равна 2 градусу в секунду, проекции угловой скорости на поперечные оси равны нулю.

Задание

  1. Построить графики изменения проекций угловой скорости ступени на связанные оси: \(\omega_x, \omega_y, \omega_z\).
  2. Построить графики изменения координат и проекций скорости центра масс ступени на оси орбитальной подвижной системы координат: \(x,y,z\), \(V_x, V_y, V_z\).
  3. Построить графики изменения углов: \(\varphi_1, \varphi_2, \varphi_3\).
  4. Определить проекции единичного вектора направление вектора кинетического момента ступени после окончания работы реактивного сопла (через 30 секунд после начала движения) в орбитальной подвижной системе \(O x_0 y_0 z_0\).
  5. Определить угол нутации и угловую скорость прецессии орбитальной ступени после окончания работы реактивного сопла (через 30 секунд после начала движения).
  6. В течение 10 секунд после окончания работы реактивного сопла (с 30 по 40 секунду после начала движения) сравнить численное и аналитические решения для проекций угловой скорости ступени, используя общее аналитическое решение для случай Эйлера (построить аналитическое решение для начальных условий \(\omega_x^0 = \omega_x(30), \omega_y^0 = \omega_y(30), \omega_z^0 =\omega_z(30)\) и сравнить его с продолжением численного решения до t = 40 c).

Методические указания

Пример MATLAB-кода для углов Брайнта (123)

Главный файл-скрипт для запуска процесса интегрирования

% Масса
params.m = 5000.0;
% Матрица тензора инерции
params.J = [5000.0,     0,     0;
            0     , 20000,     0;
            0     , 0    , 20000];
% Матрица обратная матрице тензора инерции
params.invJ = inv(params.J);

% Функция силы от времени
% Текущее значение силы интерполируется по таблице значений
% при помощи функции interp1
params.sopForceTable = @(t) interp1([0 5 10 15 30 50],[1000 380 150 50 0 0],t);

% Точка приложения силы в ССК                     
params.pFsop = [1.5; 
                1.0*sin(45*pi/180.0); 
                1.0*cos(45*pi/180.0)];  
            
% Единичный вектор направления силы в ССК
params.nFsop = [-cos(20*pi/180.0); 
                +sin(20*pi/180.0)*cos(55*pi/180.0);
                -sin(20*pi/180.0)*cos(35*pi/180.0)];                    
% Начальные условия
% Положение центра масс
r0 = [0;0;0];
% Скорость центра масс
v0 = [0;0;0];
% Начальная ориентация (углы Брайнта 1-2-3)
a0 = [0;0;0];
% Начальная угловая скорость
w0 = [0;0;0];

% Начальный вектор состояния
q0 = [r0;a0;v0;w0];
% Интервал интегрирования от 0 до 30 секунд с шагом 0.2 с
% Другой вариант (с заданным количеством точек) linspace(0,30,100)
% 100 точек в интервале от 0 до 30 с
tspan = 0:0.2:30;

% Относительная погрешность
option = odeset('RelTol',1e-8);

% Запуск процесса интегрирования дифференциальных уравнений
[t, q] = ode45(@(t,q) dqdt_orbital_stage(t,q,params), tspan, q0, option);

Файл-функция правых частей

function dq = dqdt_orbital_stage(t,q,params)
%dqdt_orbital_stage.m Файл-функция правых частей дифференциальных уравнений 
% движения орбитальной ступени

  r = q(1:3);   % Положение центра масс
  a = q(4:6);   % Углы Брайнта
  v = q(7:9);   % Скорость центра масс
  w = q(10:12); % Угловая скорость

% Матрица преобразования координат из 
% связанной системы координат (ССК) 
% в орбитальную (ОСК)
A = Axyz(a(1),a(2),a(3));

% Модуль силы
F = params.sopForceTable(t);

% Вектор силы в ССК
% Значение * единичный вектор направления
Fsop_b = F*params.nFsop;

% Вектор момента этой силы относительно ССК
Msop_b = cross(params.pFsop, Fsop_b);

% Вектор силы в ИСК
Fsop_0 = A*Fsop_b;

% Ускорение центра масс
dv = Fsop_0/params.m;

% Угловое ускорение 
dw = params.invJ*(Msop_b - cross(w,params.J*w));

% Кинематические уравнения для углов Брайнта
% (производные углов)
da = kinematicEq123(a, w);

% Собираем ответ 
% Значение правой части системы ДУ
dq = [v; da; dv; dw];

end

Функция вычисления производных углов Брайнта (функция кинематических уравнений)

function da = kinematicEq123(a, w)
%kinematicEq123.m Кинематические уравнения для углов Брайнта
% Последовательность XY'Z'' (пассивная точка зрения)
% 
% Аргументы:
%   a - строка или столбец углов Брайнта в радианах  
%   w - строка или столбец угловых скоростей радиан/с
% Результат:
%   res - столбец производных углов Брайнта
% 
     c3 = cos(a(3));
     s3 = sin(a(3));
     c2 = cos(a(2));
     s2 = sin(a(2));
     
     da = [ w(1)*c3/c2 - w(2)*s3/c2;
            w(1)*s3 + w(2)*c3;
           -w(1)*c3*s2/c2 + w(2)*s3*s2/c2 + w(3)];
end

Файл-функция Axyz.m

function A = Axyz(a1, a2, a3)
  A = Ax(a1)*Ay(a2)*Az(a3);
end

function A = Ax(angle)
  c = cos(angle);
  s = sin(angle);
  A = [1,  0,  0;
       0,  c, -s;
       0,  s,  c];
end

function A = Ay(angle)
  c = cos(angle);
  s = sin(angle);
  A = [c,  0,  s;
       0,  1,  0;
      -s,  0,  c];
end

function A = Az(angle)
  c = cos(angle);
  s = sin(angle);
  A = [c, -s,  0;
       s,  c,  0;
       0,  0,  1];
end

© 2024. All rights reserved.

Powered by Hydejack v9.1.6